Partially ordered set
A non-empty set on which some order relation is given.
Examples of partially-ordered sets. 1) The set of natural numbers with the usual order relation. 2) The set of natural numbers, where $ a \leq b $ means that $ a $ divides $ b $. 3) The set of all subsets of some set, where $ a \leq b $ means that $ a \subseteq b $. 4) The set of all real-valued functions on the interval $ [ 0 , 1 ] $, where $ f \leq g $ means that $ f ( t) \leq g ( t) $ for all $ t \in [ 0 , 1 ] $. 5) The set of all finite increasing sequences of natural numbers, where
$$ ( a _ {1} \dots a _ {k} ) \leq ( b _ {1} \dots b _ {l} ) $$
means that $ k \leq l $ and $ a _ {i} = b _ {i} $ for $ 1 \leq i \leq k $( cf. Tree). 6) An arbitrary non-empty set, where $ a \leq b $ means that $ a = b $( such a set is called a trivial or discrete partially ordered set).
Every partially ordered set $ P $ can be considered as a small category, whose objects are the elements of $ P $ and in which the set of morphisms $ H ( a , b ) $ consists of one element if $ a \leq b $ and is empty otherwise. Conversely, every small category in which $ H ( a , b ) \cup H( b, a) $ contains at most one element for each pair of objects $ ( a, b) $ is equivalent to the category of a partially-ordered set.
If one defines the relation $ \geq $ on a partially ordered set $ P $ by putting $ a \geq b $ whenever $ b \leq a $, then this relation also turns out to be an order relation. The resulting set is said to be the opposite or dual partially ordered set to $ P $.
A mapping $ \phi $ from a partially ordered set $ P $ into a partially ordered set $ P ^ \prime $ is called isotone (antitone), or an (anti-) homomorphism, if $ a \leq b $ in $ P $ implies
$$ \phi ( a) \leq \phi ( b) \ \ ( \phi ( b) \leq \phi ( a)) $$
in $ P ^ \prime $. A bijective (anti-) homomorphism is called an (anti-) isomorphism. The identity mapping of a partially ordered set $ P $ onto itself is an anti-isomorphism between $ P $ and its dual. An isomorphism is a special case of a residual mapping. The composite of two anti-homomorphisms is a homomorphism. The collection of all partially ordered sets forms a category if the isotone mappings are taken as morphisms. Every non-empty subset of a partially ordered set is a partially ordered set with respect to the induced order relation.
If $ A $ is a non-empty subset of a partially ordered set $ P $, then the lower cone $ A ^ \nabla $( the upper cone $ A ^ \Delta $) is defined to be the set of all elements $ x \in P $ such that $ x \leq a $( $ a \leq x $) for all $ a \in A $. If $ a , b \in P $ and $ a \leq b $, the subset
$$ [ a , b ] = a ^ \Delta \cap b ^ \nabla = \ \{ {x } : {a \leq x \leq b } \} $$
is called an interval or segment. The cones $ a ^ \Delta $ and $ a ^ \nabla $, $ a \in P $, are often called intervals also. An element $ u $ of a subset $ A $ is called greatest (least) if $ a \leq u $( $ u \leq a $) for all $ a \in A $. In this case $ u $ is the unique element in the intersection $ A \cup A ^ \Delta $( $ A \cap A ^ \nabla $). A greatest (least) element of a partially ordered set $ P $( if it exists) is called a unit (a zero) of $ P $, and is denoted by $ 1 $. An element $ m $ of a subset $ A $ is called maximal (minimal) if, for any element $ x \in A $, $ m \leq x $( $ x \leq m $) only if $ m = x $. In other words
$$ m ^ \Delta \cap A = m \ \ ( m ^ \nabla \cap A = m ) . $$
A greatest (least) element is maximal (minimal). The converse does not always hold. A least (greatest) element of the upper (lower) cone $ A ^ \Delta $( $ A ^ \nabla $) is called a least upper (greatest lower) bound of the subset $ A $, and is denoted by $ \sup A $( $ \inf A $). Rewriting this definition, one can say that $ u = \sup A $ if $ u \geq a $ for all $ a \in A $ and if $ u ^ \prime \geq u $ whenever $ u ^ \prime \geq a $ for all $ a \in A $. There is an analogous way of rewriting the definition of $ \inf A $. If $ P $ is a chain, then the last condition may be expressed thus; "… and if u'<a0 for some a0 A whenever u'< u" , as is usual in mathematical analysis. Elements of $ A ^ \Delta $( $ A ^ \nabla $) are often called upper (lower) bounds for the subset $ A $. It is clear that $ 1 = \sup P $ and $ 0 = \inf P $. It is a common convention that $ \sup \emptyset = 0 $ and $ \inf \emptyset = 1 $. The following properties hold:
a) if $ A \subseteq B $, then $ B ^ \Delta \subseteq A ^ \Delta $ and $ B ^ \nabla \subseteq A ^ \nabla $;
b) $ A \subseteq A ^ {\Delta \nabla } \cap A ^ {\nabla \Delta } $;
c) $ A ^ \Delta = A ^ {\Delta \nabla \Delta } $ and $ A ^ \nabla = A ^ {\nabla \Delta \nabla } $;
d) $ ( A \cup B ) ^ \Delta = A ^ \Delta \cap B ^ \Delta $;
e) $ ( A \cup B ) ^ \nabla = A ^ \nabla \cap B ^ \nabla $;
f) if $ \sup A $ or $ \inf A ^ \Delta $ exists, then $ \sup A = \inf A ^ \Delta $;
g) if $ \inf A $ or $ \sup A ^ \nabla $ exists, then $ \inf A = \sup A ^ \nabla $;
h) (generalized associativity) if $ \{ {A _ \alpha } : {\alpha \in I } \} $ is a set of subsets of a partially ordered set $ P $ and if $ \sup ( \cup _ \alpha A _ \alpha ) $ and $ \sup A _ \alpha $( $ \inf ( \cup _ \alpha A _ \alpha ) $ and $ \inf A _ \alpha $) exist for all $ \alpha \in I $, then
$$ \sup ( \cup _ \alpha A _ \alpha ) = \sup \{ \sup A _ \alpha \} , $$
$$ ( \inf ( \cup _ \alpha A _ \alpha ) = \ \inf \{ \inf A _ \alpha \} ) ; $$
i) if $ \phi $ is an isotone mapping from a partially ordered set $ P $ into a partially ordered set $ P ^ \prime $, if $ A \subseteq P $ and if both $ \sup A $ in $ P $ and $ \sup \phi ( A) $ in $ P ^ \prime $( $ \inf A $ in $ P $ and $ \inf \phi ( A) $ in $ P ^ \prime $) exist, then $ \sup \phi ( A) \leq \phi ( \sup A ) $( $ \phi ( \inf A ) \leq \inf \phi ( A) $).
Some of the definitions and results introduced above may be obtained from one another by changing the symbol $ \leq $ to $ \geq $. This applies, for example, to the definitions of upper and lower cones, and those of greatest and least elements. Such concepts are said to be dual. In particular, the statements d) and e) are dual, as are f) and g). This is all expressed in the general duality principle (cf. Duality principle in partially ordered sets).
Special forms of partially ordered sets are totally ordered sets (or chains), well-ordered sets, directed sets, lattices, semi-lattices, and Boolean algebras (cf. Boolean algebra; Directed set; Lattice; Semi-lattice; Totally ordered set; Well-ordered set). A special role is played by algebraic structures that are also partially ordered sets (cf. Ordered semi-group; Partially ordered group; Ordered ring). The concept of a partially ordered set is one of the most fundamentals notions in general mathematics, and is used extensively, both in mathematics itself and in its applications.
The definition of a partially ordered set was first clearly formulated by F. Hausdorff [11], although the axioms appearing in the definition of an order relation had been considered by G. Leibniz around 1690. An accurate definition of a totally ordered set was first given by G. Cantor [10]. In the same work he defined the order type of a totally ordered set, that is, in modern terminology, the class of all totally ordered sets isomorphic to a given one. Even earlier, Cantor had considered well-ordered sets [9], although the definition he gave does not agree with the modern one. An original approach to the axiomatic definition of totally ordered sets was presented by S.O. Shatunovskii [6], [7]. Ordered sets were used by Shatunovskii [8], and also by E.H. Moore and H.L. Smith [12], in connection with the general definition of limit in mathematical analysis.
See also the references [6]–[9] to Lattice.
References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French) |
| [3] | A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian) |
| [4] | V.V. Rozen, "Partial operations on ordered sets" , Saratov (1973) (In Russian) |
| [5] | L.A. Skornyakov, "Elements of lattice theory" , A. Hilger (1977) (Translated from Russian) |
| [6] | S.O. Shatunovskii, Zap. Novoross. Obshch. Estestvoispytatelei , 26 (1904) pp. 21–25 |
| [7] | S.O. Shatunovskii, , Proc. 1-st All-Russian Congress of Mathematics Teachers , 1 (1913) pp. 276–281 (In Russian) |
| [8] | S.O. Shatunovskii, "Introduction to analysis" , Odessa (1923) (In Russian) |
| [9] | G. Cantor, "Ueber unendliche Punktmannigfaltigkeiten, V" Math. Ann. , 21 (1883) pp. 545–591 |
| [10] | G. Cantor, "Beiträge zur Begründung der transfiniten Mengenlehre, I" Math. Ann. , 46 (1895) pp. 481–512 |
| [11] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [12] | E.H. Moore, H.L. Smith, "A general theory of limits" Amer. J. Math. , 44 (1922) pp. 102–121 |
Comments
A partially ordered set, or poset, is said to satisfy the maximum condition if every chain of increasing elements stabilizes, i.e. if $ a _ {1} \leq a _ {2} \leq \dots $, then $ a _ {n} = a _ {m} $ for all large enough $ n> m $. Such a set is also called a Noetherian poset. Dually one has the minimum condition and an Artinian poset.
The words join and meet (or supremum and infimum) are often used in place of "least upper bound" and "greatest lower bound" , respectively.
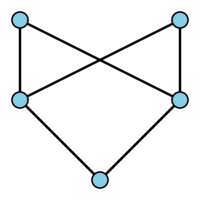
A useful pictorial representation of a finite partially ordered set is provided by its Hasse diagram, which is a graph having one vertex for each element of the underlying set, and an edge joining the vertices corresponding to elements $ a $ and $ b $( with $ b $ represented higher up the page than a) if $ a < b $ but there is no element $ c $ with $ a < c < b $. (Here "a< b" means, as usual, "a≤ b but a≠ b" ). For example, the diagram below represents a certain five-element partially ordered set having a least element but no greatest element.
From such a diagram the entire order relation may be read off using transitivity: $ a \leq b $ if and only if there is a raising path from the vertex corresponding to $ a $ to that corresponding to $ b $.
The applied theory of partial order is of very much more mathematical interest than the pure. Partial orderings arise naturally in all branches of mathematics. Broadly, there are two principal types of partially ordered sets of mathematical objects: partial solutions of problems, ordered by consistent extension — here one wants a maximal, indeed a complete, solution; and diagrams of related objects, for which the aim is not to cross it but to analyze it.
Choice and dependent choice.
Probably a majority of the applications of the axiom of choice involve one of the order-theoretic versions of the axiom. These are mainly: $ \alpha $) the maximality principle (also called the Zorn lemma): If a partially ordered set $ X $ includes an upper bound of each of its totally ordered subsets, then $ X $ has a maximal element. $ \beta $) A variant form: Each partially ordered set contains a maximal totally ordered subset. $ \gamma $) The Teichmüller–Tukey principle: If a family of conditions on partial functions from $ A $ to $ B $ concerns only their values on finite subsets of $ A $, then there is a maximal partial function satisfying these conditions. Each of $ \alpha $)– $ \gamma $) is equivalent to the axiom of choice.
The principle of dependent choice (Brouwer's infinity lemma, König's selection theorem) is this. Suppose given an infinite sequence of non-empty finite sets $ S _ {n} $, and a relation $ R $ true for certain pairs $ ( x, y) $, where $ x \in S _ {n} $ and $ y \in S _ {n+} 1 $. Suppose that for each $ y \in S _ {n+} 1 $, $ R( x, y) $ is true for at least one $ x $. Then there exists a sequence $ ( x _ {n} ) $, $ x _ {n} \in S _ {n} $, such that $ R( x _ {n} , x _ {n+} 1 ) $ is true for all $ n $. A classic application of dependent choice is to colouring in four colours an infinite planar map $ M $. Enumerate the regions of $ M $ in any order; let $ M _ {n} $ be the submap composed of the first $ n $ regions; let $ S _ {n} $ be the set of admissible colourings of $ M _ {n} $. The relation $ R $ is extension; each colouring of $ M _ {n+} 1 $ extends a (unique) colouring of $ M _ {n} $. By the four-colour theorem (cf. Graph colouring; Four-colour problem), each $ S _ {n} $ is non-empty. Accordingly there is a sequence $ ( x _ {n} ) $ of colourings of the submaps $ M _ {n} $ which is consistent, since each $ x _ {n+} 1 $ is an extension of $ x _ {n} $. This determines a colouring of $ M $.
Combinatorics.
In the combinatorics of ordered objects or diagrams of objects, usually the role of the partial order is inseparable, or separable only unnaturally, from the rest of the structure. There is a neat illustration in the series of nine papers "On the foundations of combinatorial theory. I–IX" , published by G.C. Rota and collaborators in 1964–1974. Paper I [a4] is subtitled "Theory of Möbius functions" . The Möbius function of a (finite, or locally finite in a suitable sense) partially ordered set $ X $ is an integer-valued function $ \mu $ of two variables $ x, y \in X $, which is 0 unless $ x \leq y $. The characteristic property is that, like the number-theoretic Möbius function, it inverts the process of summing a function $ f: X \rightarrow G $ with values in an additive group, to the sum $ f ^ { * } : X \rightarrow G $ defined by $ f ^ { * } ( y) = \sum [ f( x) : x \leq y ] $; the formula is $ f( y) = \sum [ f ^ { * } ( x) \mu ( x, y) : x \leq y ] $. These Möbius functions recur often in the rest of the series and in many other places.
One of the fundamental theorems of combinatorics is, exceptionally, in pure order theory. That is the theorem of R. Dilworth: A partially ordered set is the union of $ n $ totally ordered subsets if and only if it contains no $ n+ 1 $ pairwise incomparable elements. In combinatorial analysis this theorem is mentioned, but it is bracketed with P. Hall's theorem on systems of distinct representatives. Note the radical difference: Dilworth's theorem is true for arbitrary partially ordered sets, the number $ n $ being finite [a2]. Hall's theorem applies only to systems of distinct representatives of families of finite sets. For the relationships of Dilworth's theorem, see [a1].
Sometimes the nature of a naturally occurring partial order is the central problem. For instance, much study has been devoted to extensions of Kuratowski's theorem that the set of topological types of non-planar finite graphs, ordered by imbeddability, has just two minimal elements. (See Graph, planar; Graph theory.) Here, as in many cases, the naturally given order relation is only a quasi-ordering (cf. Pre-order), i.e. a reflexive, transitive relation. Every quasi-ordering of a set $ X $ determines a partial ordering on the equivalence classes of the equivalence relation "x≤ y and y≤ x" . Accordingly one is interested in well-quasi-ordered sets: sets $ X $ with a quasi-ordering under which $ X $ contains no infinite pairwise incomparable set and no infinite strictly-decreasing sequence. Then in the associated partially ordered set of equivalence classes, the set of minimal elements of each non-empty subset is non-empty and finite. N. Robertson and P. Seymour have announced the theorem — extending a number of previous results — that finite graphs are well-quasi-ordered by the relation of containment as a minor. (Here a minor of a graph $ G $ is a graph that can be obtained from a subgraph of $ G $ by contracting edges.) The proof is emerging in a long series of papers; the subtitles of the first nine are given in the announcement [a3], and six of them have so far (1989) been published.
Well-quasi-ordering is the beginning of the combinatorics of infinite partially ordered sets, a division of set theory which has some impressive results but relatively little connection with most of mathematics. However, another aspect of infinite partially ordered sets is fundamental for topology and functional analysis: this is convergence of nets. (See Net (directed set).) The role of subsequences in ordinary convergence of sequences is taken by subnets, which are carried by convergent mappings between directed sets; that is, mappings $ f: D \rightarrow E $ such that the image of every cofinal subset of $ D $ is cofinal in $ E $. The use of cofinal subsets $ D \subset E $ is not sufficient (as it is for sequences). However, one has the theorem of J.W. Tukey: If $ D $ and $ E $ are directed sets for which there are convergent mappings $ f: D \rightarrow E $ and $ g: E \rightarrow D $, then there exists a directed set $ F $ in which both $ D $ and $ E $ can be imbedded as cofinal subsets (and conversely). In this case $ D $ and $ E $ are said to be cofinally similar, or of the same cofinal type.
The classification of cofinal types is in a primitive state. All countable directed sets without a greatest element are of one cofinal type. The main further results known are: A) it is consistent with the axioms of set theory (ZFC) that there are only three more cofinal types represented by directed sets of power $ \aleph _ {1} $( namely $ \omega _ {1} $, $ \omega _ {0} \times \omega _ {1} $, and the set of finite subsets of $ \omega _ {1} $); but B) there are $ 2 ^ {\mathfrak c } $ different cofinal types of directed sets of the power of the continuum $ {\mathfrak c } $, see [a5].
References
| [a1] | M. Aigner, "Combinatorial theory" , Springer (1979) (Translated from German) Zbl 0415.05001 |
| [a2] | R.P. Dilworth, "A decomposition theorem for partially ordered sets" Ann. Math. (2) , 51 (1950) pp. 161–166 Zbl 0038.02003 |
| [a3] | N. Robertson, P.D. Seymour, "Graph minors - a survey" I. Anderson (ed.) , Surveys in Combinatorics 1985 , Cambridge Univ. Press (1985) pp. 153–171 |
| [a4] | G.C. Rota, "On the foundations of combinatorial theory. I: Theory of Möbius functions" Z. Wahrsch. , 2 (1964) pp. 340–368 |
| [a5] | S. Todorčević, "Directed nets and cofinal types" Trans. Amer. Math. Soc. , 290 (1985) pp. 711–723 |
| [a6] | G. Grätzer, "General lattice theory" , Birkhäuser (1978) (Original: Lattice theory. First concepts and distributive lattices. Freeman, 1978) |
Partially ordered set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partially_ordered_set&oldid=52964