Convex function (of a complex variable)
A regular univalent function
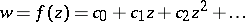 |
in the unit disc 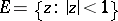 mapping the unit disc onto some convex domain. A regular univalent function
mapping the unit disc onto some convex domain. A regular univalent function 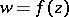 is a convex function if and only if the tangent to the image of
is a convex function if and only if the tangent to the image of  ,
, 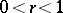 , at the point
, at the point 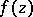 rotates only in one direction as the circle is traversed. The following inequality expresses a necessary and sufficient condition for convexity of
rotates only in one direction as the circle is traversed. The following inequality expresses a necessary and sufficient condition for convexity of 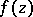 :
:
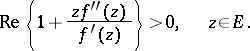 | (1) |
On the other hand, 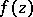 is a convex function if and only if it can be parametrically expressed as follows:
is a convex function if and only if it can be parametrically expressed as follows:
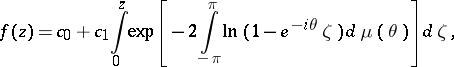 | (2) |
where 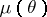 is a non-decreasing real-valued function on
is a non-decreasing real-valued function on 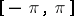 such that
such that
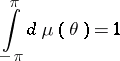 |
and 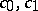 are complex constants,
are complex constants, 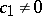 . Formula (2) can be regarded as a generalization of the Christoffel–Schwarz formula for mappings of the disc
. Formula (2) can be regarded as a generalization of the Christoffel–Schwarz formula for mappings of the disc 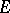 onto convex polygons.
onto convex polygons.
Let 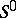 be the class of all convex functions in
be the class of all convex functions in  normalized by the conditions
normalized by the conditions 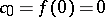 ,
,  ; let
; let 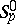 ,
, 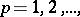 be the subclasses of
be the subclasses of 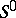 consisting of functions that map
consisting of functions that map 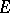 onto convex domains of the
onto convex domains of the 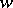 -plane with a
-plane with a 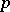 -fold symmetry of rotation about the point
-fold symmetry of rotation about the point  ,
, 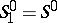 . The classes
. The classes 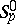 are compact with respect to uniform convergence on compact sets inside
are compact with respect to uniform convergence on compact sets inside 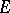 . Their integral representations, in particular formula (2) for
. Their integral representations, in particular formula (2) for 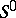 , make it possible to develop variational methods for the solution of extremal problems in the classes
, make it possible to develop variational methods for the solution of extremal problems in the classes 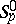 [2], [3], [4], [5].
[2], [3], [4], [5].
Fundamental extremal properties of 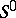 may be described by the following sharp inequalities:
may be described by the following sharp inequalities:
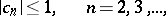 |
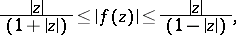 |
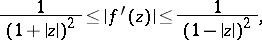 |
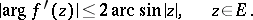 |
The argument of the function is understood to mean the branch that vanishes if 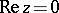 . In all these estimates the equality sign holds for the function
. In all these estimates the equality sign holds for the function 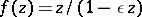 ,
,  , only. Sharp bounds are also available for the ratio
, only. Sharp bounds are also available for the ratio 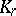 between the curvature
between the curvature  of the boundary
of the boundary 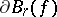 of the domain
of the domain 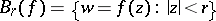 on the class
on the class 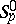 ,
, 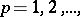 at the point
at the point 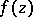 and the curvature
and the curvature 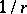 of the pre-image of
of the pre-image of 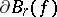 , i.e. the circle
, i.e. the circle  at the point
at the point  . The disc
. The disc 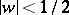 belongs to the domains
belongs to the domains 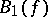 ,
, 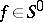 , and the radius of this circle cannot be increased without imposing additional restrictions on the class of functions. If
, and the radius of this circle cannot be increased without imposing additional restrictions on the class of functions. If 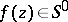 , the univalent function
, the univalent function 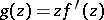 will be star-shaped in
will be star-shaped in 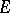 , i.e. will map
, i.e. will map 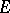 onto a domain that is star-shaped with respect to the coordinate origin.
onto a domain that is star-shaped with respect to the coordinate origin.
Examples of generalizations and modifications of the class 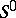 and its subclasses include: the class
and its subclasses include: the class 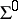 of functions
of functions 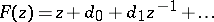 univalent in
univalent in 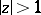 , regular for
, regular for 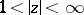 and mapping
and mapping 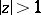 onto a domain with a convex complement; the class
onto a domain with a convex complement; the class 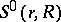 of functions
of functions 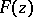 regular in the annulus
regular in the annulus 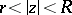 and normalized in a certain manner, each one of them mapping this annulus univalently onto a domain such that the finite component of its complement is convex and its union with this component is convex as well; and the class
and normalized in a certain manner, each one of them mapping this annulus univalently onto a domain such that the finite component of its complement is convex and its union with this component is convex as well; and the class 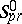 of functions in
of functions in 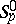 with real coefficients in the Taylor series in a neighbourhood of the point
with real coefficients in the Taylor series in a neighbourhood of the point 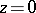 . The concept of a convex function can be extended to multi-valent functions (cf. [2], Appendix).
. The concept of a convex function can be extended to multi-valent functions (cf. [2], Appendix).
Of independent interest is the following generalization of a convex function [6]: A function 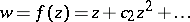 regular in the disc
regular in the disc 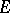 is called close-to-convex if there exists a convex function
is called close-to-convex if there exists a convex function 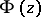 ,
, 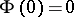 , on
, on 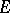 such that, everywhere in
such that, everywhere in 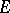 ,
,
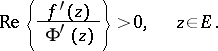 |
It has been proved that all functions 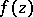 in this class
in this class  are univalent, and necessary and sufficient conditions for a function
are univalent, and necessary and sufficient conditions for a function 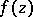 to belong to
to belong to 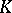 have been found. The parametric representation of functions
have been found. The parametric representation of functions 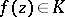 with the aid of Stieltjes integrals is
with the aid of Stieltjes integrals is
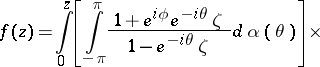 |
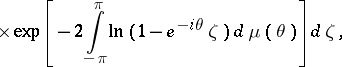 |
where 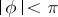 and
and 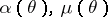 are non-decreasing real-valued functions with
are non-decreasing real-valued functions with
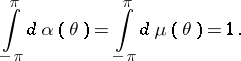 |
The class 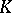 includes convex, star-shaped and other functions. The Bieberbach conjecture,
includes convex, star-shaped and other functions. The Bieberbach conjecture, 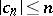 , is valid for functions
, is valid for functions  . The following sharp estimates are known:
. The following sharp estimates are known:
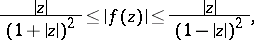 |
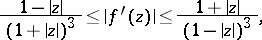 |
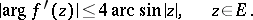 |
The argument of a function is understood to mean the branch that vanishes if 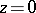 . In all these estimates the equality sign holds for the function
. In all these estimates the equality sign holds for the function 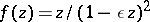 ,
,  , only. Geometrically, functions
, only. Geometrically, functions  of class K are characterized by the fact that they map the disc
of class K are characterized by the fact that they map the disc 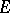 onto domains
onto domains 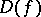 whose exterior
whose exterior 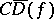 can be filled by rays
can be filled by rays 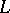 drawn from points on the boundary of the domain,
drawn from points on the boundary of the domain, 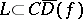 . The concept of a close-to-convex function has been extended to multi-valent functions [7].
. The concept of a close-to-convex function has been extended to multi-valent functions [7].
References
| [1] | I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1958–1959) (Translated from Russian) |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | V.A. Zmorovich, "On some variational problems in the theory of univalent functions" Ukrain. Math. Zh. , 4 : 3 (1952) pp. 276–298 (In Russian) |
| [4] | I.A. Aleksandrov, V.V. Chernikov, "Extremal properties of star-shaped mappings" Sibirsk. Mat. Zh. , 4 : 2 (1963) pp. 261–267 (In Russian) |
| [5] | V.A. Zmorovich, "On certain classes of analytic functions, univalent in an annulus" Mat. Sb. , 32 (74) : 3 (1953) pp. 633–652 (In Russian) |
| [6] | W. Kaplan, "Close-to-convex schlicht functions" Michigan Math. J. , 1 (1952) pp. 169–185 |
| [7] | D. Styer, "Close-to-convex multivalued functions with respect to weakly starlike functions" Trans. Amer. Math. Soc. , 169 (1972) pp. 105–112 |
Comments
With the phrase "sharp estimatesharp estimate" is meant an estimate which cannot be improved (as is usual in complex analysis).
The Bieberbach conjecture has been proved for arbitrary (normalized) univalent functions in 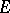 , see Bieberbach conjecture and the references to it.
, see Bieberbach conjecture and the references to it.
Convex function (of a complex variable). I.A. AleksandrovYu.D. Maksimov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_function_(of_a_complex_variable)&oldid=14229