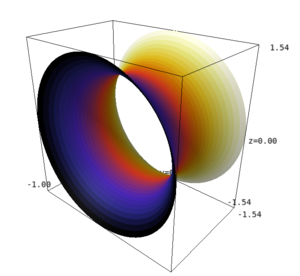
Catenoid
2020 Mathematics Subject Classification: Primary: 53A10 Secondary: 49Q05 [MSN][ZBL]
The surface formed by the revolution of a catenary $y=c\cosh x/c$ about the $x$-axis, where $c$ is a positive constant. The parametric equations for the catenoid are then \[ x = v \quad y = c \cosh \frac{v}{c} \sin u \quad z = c \cosh \frac{v}{c} \cos u\, . \] The catenoid is a minimal surface and it is the form realized by a soap film "stretched" over two wire discs the planes of which are perpendicular to the line joining their centres (see Fig. 1). The catenoid is a member of the one-parameter family of surfaces of revolution of the curves $y = a \cosh x/b$, which are sometimes also called catenoids. However only for the special choice of parameters $a = b$ the corresponding surface is a minimal surface and usually the word catenoid is used only for this particular case.
The catenoid is locally isometric to the helicoid and in fact such local isometry can be achieved as endpoint of a continuous one-parameter family of isometric deformations which are all minimal surfaces.
References
| [BG] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) MR0917479 Zbl 0629.53001 |
| [DoC] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1975) pp. 214 Zbl 0733.53001 Zbl 0606.53002 Zbl 0326.53001 |
| [Hs] | C.C. Hsiung, "A first course in differential geometry" , Wiley (Interscience) (1981) |
| [ON] | B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) Zbl 0971.53500 Zbl 0974.53001 |
| [Sp] | M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 218–219 MR0532834 MR0532833 MR0532832 MR0532831 MR0532830 MR0394453 MR0394452 MR0372756 MR1537051 MR0271845 MR0267467 Zbl 1213.53001 Zbl 0439.53005 Zbl 0439.53004 Zbl 0439.53003 Zbl 0439.53002 Zbl 0439.53001 Zbl 0306.53003 Zbl 0306.53002 Zbl 0306.53001 Zbl 0202.52201 Zbl 0202.52001 |
Catenoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Catenoid&oldid=54430