Three-sigma rule
A rule of thumb, according to which, in certain problems in probability theory and mathematical statistics, an event is considered to be practically impossible if it lies in the region of values of the normal distribution of a random variable at a distance from its mathematical expectation of more than three times the standard deviation.
Let  be a normally
be a normally  distributed random variable. For any
distributed random variable. For any  ,
,
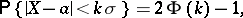 |
where  is the distribution function of the standard normal law; whence, in particular, for
is the distribution function of the standard normal law; whence, in particular, for  it follows that
it follows that
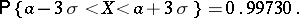 |
The latter equation means that the values of 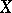 can differ from its expectation
can differ from its expectation  by a quantity exceeding
by a quantity exceeding 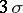 on the average in not more than 3 times in a thousand trials. This circumstance is sometimes used by an experimenter in certain problems of probability theory and mathematical statistics, by assuming that the event
on the average in not more than 3 times in a thousand trials. This circumstance is sometimes used by an experimenter in certain problems of probability theory and mathematical statistics, by assuming that the event 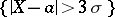 is practically impossible and, consequently, the event
is practically impossible and, consequently, the event  is practically certain. In this case one says that the experimenter has applied the "three-sigma" rule.
is practically certain. In this case one says that the experimenter has applied the "three-sigma" rule.
References
| [1] | N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian) |
Three-sigma rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Three-sigma_rule&oldid=17366