Sierpiński gasket
tamis de Sierpiński
The Sierpiński gasket (in French: "tamis de Sierpiński" ) — along with its companion, the Sierpiński carpet, or "tapis de Sierpiński" — belongs to the toolkit of every fractal geometer. It adorns many articles and books on the subject and is frequently used as an example or test case in various mathematical and physical studies of self-similarity. Although it is geometrically more complex than the classic Cantor set, it is still one of the simplest interesting fractals. It was introduced in 1915 [a38] by the Polish mathematician W. Sierpiński, about forty years after the discovery of the Cantor set.
Like other self-similar fractals, the Sierpiński gasket is constructed iteratively. Beginning with an equilateral triangle, an inverted triangle with half the side-length of the original is removed. This process is then repeated with each of the remaining triangles ad infinitum (see Fig.a1).

Figure: s130310a
The Sierpiński pre-gaskets (left) and the Sierpiński gasket (right)
Unlike the ternary Cantor set, which is a totally disconnected and compact subset of the real line (and hence has topological dimension zero [a10], cf. also Zero-dimensional space; Totally-disconnected space), the Sierpiński gasket is a connected compact subset of the Euclidean plane $\mathbf{R}^2$ (cf. also Connected space). In fact, it can be viewed as a simple, continuous and closed plane curve (i.e., a Jordan curve); see [a38], [a42], § 3.7. Hence, it has topological dimension one [a10]. In addition, it is non-rectifiable (i.e., it is a curve of infinite length, cf. also Peano curve; Rectifiable curve).
The gasket is strictly self-similar in the sense that it can be written as a finite union of scaled copies of itself; namely, as a union of three Sierpiński gaskets, each with a side-length equal to half that of the original (see Fig.a2). More precisely, the Sierpiński gasket is the unique non-empty compact subset $G$ of the plane such that $G=\cup^3_{j=1}S_j(G)$, where $S_j$ is the similarity transformation of $\mathbf{R}^2$ with contraction ratio $1/2$ and with fixed point $v_j$, the $j$th vertex of the initial triangle in the construction of the gasket:
\begin{equation}S_j(z)=\frac{1}{2}(z-v_j)+v_j,\end{equation}
for $z\in\mathbf{R}^2$ and $j=1,2,3$. Moreover, the Hausdorff and Minkowski (or box) dimensions of the Sierpiński gasket are both equal to its similarity dimension: $\log(3)/\log(2)$ (cf. also Hausdorff dimension). This common value, $\log(3)/\log(2)\approx 1.58$, is often referred to as the fractal dimension of $G$. Here, $2$ is the reciprocal of the contraction ratio and $3$ is the number of parts of $G$ similar to the whole in that ratio (see, for example, [a7], Chapt. 9, [a11], [a32], [a27], Plate 141).
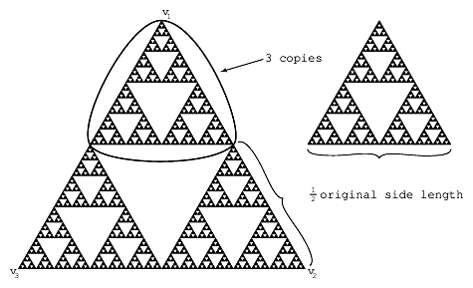
Figure: s130310b
Self-similarity of the Sierpiński gasket
It follows from the above self-similarity equation that 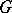 is the basin of attraction of the dynamical system formed by the mappings
is the basin of attraction of the dynamical system formed by the mappings 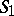 ,
,  and
and 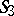 . (See [a11] or [a7], Chapt. 9.) In particular, every point of
. (See [a11] or [a7], Chapt. 9.) In particular, every point of 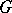 can be written (not necessarily uniquely) as a ternary string of possibly infinite length (see Fig.a3).
can be written (not necessarily uniquely) as a ternary string of possibly infinite length (see Fig.a3).
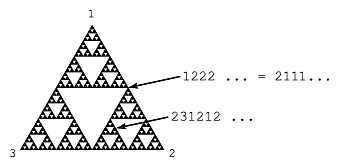
Figure: s130310c
Coding of the points of 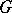
Recently (2000), it has been suggested that the oscillations intrinsic to the geometry of 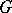 (and other self-similar fractals) can be described via suitable number-theoretic explicit formulas [a19], Chapt. 4, by means of a set of "complex dimensions" having maximum real part equal to the (real) fractal dimension. Here, the complex dimensions of
(and other self-similar fractals) can be described via suitable number-theoretic explicit formulas [a19], Chapt. 4, by means of a set of "complex dimensions" having maximum real part equal to the (real) fractal dimension. Here, the complex dimensions of 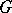 with real part
with real part 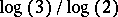 are of the form
are of the form 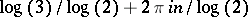 , where
, where 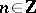 and
and 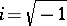 (see [a19], Chapts. 2–6 and 10, where a mathematical theory of complex dimensions is developed in the one-dimensional case).
(see [a19], Chapts. 2–6 and 10, where a mathematical theory of complex dimensions is developed in the one-dimensional case).
It is noteworthy that the self-similarity equation is analogous to that satisfied by an algebraic number; for example, 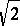 is a solution of the quadratic equation
is a solution of the quadratic equation 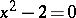 [a32], § 3.4. Thus, in a sense, fractal geometries can be viewed as extensions of ordinary (Euclidean) geometries, much like algebraic number fields are extensions of the field of rational numbers. A more precise analogy is developed in [a19], Chapt. 2 (and the relevant references therein), where the corresponding dichotomy algebraic versus transcendental (or rational versus irrational) is given a concrete meaning (see also [a20], [a21]).
[a32], § 3.4. Thus, in a sense, fractal geometries can be viewed as extensions of ordinary (Euclidean) geometries, much like algebraic number fields are extensions of the field of rational numbers. A more precise analogy is developed in [a19], Chapt. 2 (and the relevant references therein), where the corresponding dichotomy algebraic versus transcendental (or rational versus irrational) is given a concrete meaning (see also [a20], [a21]).
The Sierpiński gasket is a prototypical example of a "finitely ramified fractal" . Roughly speaking, this means that it may be disconnected by removing only finitely many points; see Fig.a4. Indeed, every point of 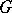 has a finite order of ramification, namely, either
has a finite order of ramification, namely, either  ,
,  or
or 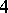 ; see [a38], [a27], Chapt. 14, or [a32], p. 118. This topological notion has been abstracted in [a14], where
; see [a38], [a27], Chapt. 14, or [a32], p. 118. This topological notion has been abstracted in [a14], where 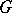 is viewed as an example of a post-critically finite (p.c.f.) self-similar set.
is viewed as an example of a post-critically finite (p.c.f.) self-similar set.
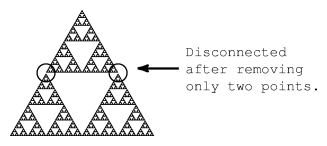
Figure: s130310d
The Sierpiński gasket is finitely ramified
Sierpiński carpet.
The Sierpiński carpet 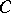 is defined analogously to the gasket. Beginning with a square, a square with one-third the side-length of the original is removed from the centre. This process is then repeated with each of the remaining squares ad infinitum.
is defined analogously to the gasket. Beginning with a square, a square with one-third the side-length of the original is removed from the centre. This process is then repeated with each of the remaining squares ad infinitum.

Figure: s130310e
The Sierpiński pre-carpets (left) and the Sierpiński carpet (right)
From Fig.a5, it is clear that the medians and diagonals of the original square intersect 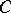 in a Cantor set; in fact,
in a Cantor set; in fact, 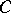 can be thought of as a natural analogue of the Cantor set in the plane. The Sierpiński carpet is also a strictly self-similar fractal: it is the union of eight copies of itself, scaled in the contraction ratio
can be thought of as a natural analogue of the Cantor set in the plane. The Sierpiński carpet is also a strictly self-similar fractal: it is the union of eight copies of itself, scaled in the contraction ratio 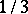 (see Fig.a6). Therefore, its fractal dimension is equal to
(see Fig.a6). Therefore, its fractal dimension is equal to 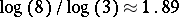 , the similarity dimension of
, the similarity dimension of 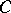 (see [a7], [a27] or [a32]).
(see [a7], [a27] or [a32]).
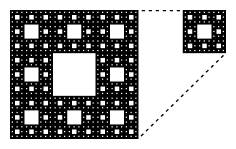
Figure: s130310f
Self-similarity of the Sierpiński carpet
Unlike the Sierpiński gasket, however, the Sierpiński carpet is infinitely ramified, as can be easily seen from Fig.a5 or Fig.a6. Actually, one needs to remove uncountably many points in order to disconnect 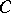 . This topological property has interesting physical consequences. For example, in the context of statistical physics and the theory of critical phenomena, it is expected that a phase transition occurs for Ising models (cf. Ising model) on fractal lattices such as the Sierpiński carpet but not the Sierpiński gasket (see [a27], p. 138).
. This topological property has interesting physical consequences. For example, in the context of statistical physics and the theory of critical phenomena, it is expected that a phase transition occurs for Ising models (cf. Ising model) on fractal lattices such as the Sierpiński carpet but not the Sierpiński gasket (see [a27], p. 138).
From the mathematical point of view, the most striking property of the Sierpiński carpet is its universality. Sierpiński proved in his original 1916 paper on the subject [a39] that every Jordan curve in the plane can be homeomorphically embedded in the Sierpiński carpet. Hence, for example, 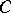 contains a homeomorphic image of the Sierpiński gasket
contains a homeomorphic image of the Sierpiński gasket 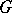 . This remarkable and underappreciated theorem was extended by the Austrian mathematician K. Menger in [a28]. For instance, the Menger sponge (the three-dimensional analogue of the Sierpiński carpet, see [a27], Plate 145) is universal for all compact (metrizable) spaces of topological dimension one, and thus for all Jordan curves in space. In addition to the original references [a39] and [a28], see [a32], § 2.7, for a helpful heuristic discussion and [a31] for an exposition of the proof of the Sierpiński–Menger theorem (see also [a29], Chapt. 9, and [a43], pp. 433; 501).
. This remarkable and underappreciated theorem was extended by the Austrian mathematician K. Menger in [a28]. For instance, the Menger sponge (the three-dimensional analogue of the Sierpiński carpet, see [a27], Plate 145) is universal for all compact (metrizable) spaces of topological dimension one, and thus for all Jordan curves in space. In addition to the original references [a39] and [a28], see [a32], § 2.7, for a helpful heuristic discussion and [a31] for an exposition of the proof of the Sierpiński–Menger theorem (see also [a29], Chapt. 9, and [a43], pp. 433; 501).
Finally, a lot of work has been recently (as of 2000) done in order to develop "analysis on fractals" , using the Sierpiński gasket (and sometimes the Sierpiński carpet) as a prototypical example. In particular, one can obtain suitable analogues of Laplacians, diffusions (or Brownian motions) and related notions on these self-similar fractals and their generalizations (see, for instance, [a2], [a3], [a4], [a8], [a9], [a13], [a14], [a15], [a16], [a17], [a18], [a22], [a23], [a24], [a25], [a40], [a41]).
Brownian motion on the Sierpiński gasket is defined as a suitably rescaled limit of random walks on the Sierpiński pre-gaskets (see, for example, [a9], [a18], [a4], [a2]). Similarly, Laplacians on the Sierpiński gasket are defined as suitably rescaled (or renormalized) limits of finite difference operators acting on an increasing sequence of finite graphs approximating 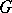 (cf. Fig.a1; see also [a13], [a14]).
(cf. Fig.a1; see also [a13], [a14]).
One can obtain an analogue of Weyl's classic asymptotic formula for the eigenvalue distribution of Laplacians on 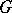 and other finitely ramified fractals (see [a16] and earlier references therein, including [a8]). One can also introduce a corresponding notion of "spectral dimension" , an appropriate analogue of the notion of fractal dimension in this context. Hence, paraphrasing M. Kac [a12], one can "hear" the spectral dimension of the Sierpiński drum and other "fractal drums" [a16]. In some sense, one can also hear the volume of
and other finitely ramified fractals (see [a16] and earlier references therein, including [a8]). One can also introduce a corresponding notion of "spectral dimension" , an appropriate analogue of the notion of fractal dimension in this context. Hence, paraphrasing M. Kac [a12], one can "hear" the spectral dimension of the Sierpiński drum and other "fractal drums" [a16]. In some sense, one can also hear the volume of 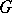 (see [a23], [a25] and [a17]). More precisely, one can introduce a suitable notion of volume measure or "spectral volume" of
(see [a23], [a25] and [a17]). More precisely, one can introduce a suitable notion of volume measure or "spectral volume" of 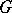 (and other finitely ramified fractals); see [a23], [a25], where (in particular, for homogeneous mass distributions) it is proposed to be an analogue for this class of fractals of the Riemannian volume measure on a Riemannian manifold. It is then shown in [a17] to be a specific self-similar measure, which, in the case of the homogeneous gasket, coincides with the natural Hausdorff measure on
(and other finitely ramified fractals); see [a23], [a25], where (in particular, for homogeneous mass distributions) it is proposed to be an analogue for this class of fractals of the Riemannian volume measure on a Riemannian manifold. It is then shown in [a17] to be a specific self-similar measure, which, in the case of the homogeneous gasket, coincides with the natural Hausdorff measure on 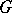 . (The proof of this fact given in [a17] makes use of the so-called "decimation method" for computing recursively the eigenvalues and the eigenfunctions of the Laplacian on
. (The proof of this fact given in [a17] makes use of the so-called "decimation method" for computing recursively the eigenvalues and the eigenfunctions of the Laplacian on 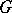 ; see [a33], [a34] in the physics literature and [a8], [a37], [a41] in the mathematics literature. It also makes use of the existence of many localized eigenfunctions on the gasket; see, for example, [a1] and [a15].) The results of [a16], [a23] and [a17] yield a precise form of Weyl's asymptotic law in this context.
; see [a33], [a34] in the physics literature and [a8], [a37], [a41] in the mathematics literature. It also makes use of the existence of many localized eigenfunctions on the gasket; see, for example, [a1] and [a15].) The results of [a16], [a23] and [a17] yield a precise form of Weyl's asymptotic law in this context.
These problems have applications in condensed matter physics and solid state physics; for example, in the study of electrical transport in porous or in random media, as well as of heat diffusion or wave propagation on fractals and in disordered systems (see, for instance, [a1], [a5], [a22], [a24], [a26], [a30], [a33], [a34], [a35], [a36]).
A number of other topics from classical harmonic analysis, probability theory, partial differential equations, mathematical physics, spectral geometry, and even number theory have (or are expected to have) interesting counterparts in this context (see, for example, [a2], [a15], [a22], [a24], [a25], [a19], [a40], and the relevant references therein). As was mentioned previously, the Sierpiński gasket is often a testing ground for conjectures concerning finitely ramified (or p.c.f.) self-similar fractals. Although several probabilistic results have been obtained for the Sierpiński carpet (and its higher-dimensional analogues) [a3], [a2], the realm of infinitely ramified fractals remains much more elusive from the analytical point of view (especially in dimension three or higher) and will no doubt be the object of many further investigations in the future.
The author is grateful to his student, E.P.J. Pearse, for his comments and for help with the preparation of the figures.
References
| [a1] | S. Alexander, R. Orbach, "Density of states on fractals: fractons" J. Physique Lettres , 43 (1982) pp. L625–L631 |
| [a2] | M.T. Barlow, "Diffusions on fractals" M.T. Barlow (ed.) D. Nualart (ed.) , Lectures in Probability Theory and Statistics, École d'Eté de Probab. de Saint Flour XXV—1996 , Lecture Notes in Mathematics , 1690 , Springer (1998) pp. 1–121 |
| [a3] | M.T. Barlow, R.F. Bass, "Construction of Brownian motion on the Sierpiński carpet" Ann. Inst. H. Poincaré , 25 (1989) pp. 225–257 |
| [a4] | M.T. Barlow, E.A. Perkins, "Brownian motion on the Sierpiński gasket" Probab. Th. Rel. Fields , 79 (1988) pp. 543–623 |
| [a5] | M.V. Berry, "Distribution of modes in fractal resonators" W. Güttinger (ed.) H. Eikemeier (ed.) , Structural Stability in Physics , Springer (1979) pp. 51–53 |
| [a6] | "Classics on fractals" G.A. Edgar (ed.) , Addison-Wesley (1993) |
| [a7] | K. Falconer, "Fractal geometry: Mathematical foundations and applications" , Wiley (1990) |
| [a8] | M. Fukushima, T. Shima, "On a spectral analysis for the Sierpiński gasket" Potential Anal. , 1 (1992) pp. 1–35 |
| [a9] | S. Goldstein, "Random walks and diffusions on fractals" H. Kesten (ed.) , Percolation Theory and Ergodic Theory of Infinite Particle Systems , IMA Math.Appl. , 8 , Springer (1987) pp. 121–129 |
| [a10] | W. Hurewicz, H. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
| [a11] | J.E. Hutchinson, "Fractals and self-similarity" Indiana Univ. Math. J. , 30 (1981) pp. 713–747 |
| [a12] | M. Kac, "Can one hear the shape of a drum?" Amer. Math. Monthly , 73 (1966) pp. 1–23 |
| [a13] | J. Kigami, "A harmonic calculus on the Sierpiński spaces" Japan J. Appl. Math. , 6 (1989) pp. 259–290 |
| [a14] | J. Kigami, "Harmonic calculus on p.c.f. self-similar sets" Trans. Amer. Math. Soc. , 335 (1993) pp. 721–755 |
| [a15] | J. Kigami, "Analysis on fractals" , Cambridge Univ. Press (in press) |
| [a16] | J. Kigami, M.L. Lapidus, "Weyl's problem for the spectral distribution of Laplacians on p.c.f. self-similar fractals" Commun. Math. Phys. , 158 (1993) pp. 93–125 |
| [a17] | J. Kigami, M.L. Lapidus, "Self-similarity of volume measures for Laplacians on p.c.f. self-similar fractals" Commun. Math. Phys. , 217 (2001) pp. 165–180 |
| [a18] | S. Kusuoka, "A diffusion process on a fractal" K. Ito (ed.) N. Ikeda (ed.) , Probabilistic Methods in Mathematical Physics, Proc. Taginuchi Internat. Symp. (Katata and Kyoto, 1985) , Kinokuniya (1987) pp. 251–274 |
| [a19] | M.L. Lapidus, M. van Frankenhuysen, "Fractal geometry and number theory (complex dimensions of fractal strings and zeros of zeta functions)" , Research Monograph , Birkhäuser (2000) |
| [a20] | M.L. Lapidus, M. van Frankenhuysen, "A prime number theorem for self-similar flows" M.L. Lapidus (ed.) M. van Frankenhuysen (ed.) , Dynamical, Spectral and Arithmetic Zeta Functions , Contemp. Math. , Amer. Math. Soc. (2001) |
| [a21] | M.L. Lapidus, M. van Frankenhuysen, "Complex dimensions of self-similar fractal strings and Diophantine approximation" Preprint (2001) |
| [a22] | M.L. Lapidus, "Vibrations of fractal drums, the Riemann hypothesis, waves in fractal media, and the Weyl–Berry conjecture" B.D. Sleeman (ed.) R.J. Jarvis (ed.) , Ordinary and Partial Differential Equations, Proc. Twelfth Internat. Conf. (Dundee, Scotland, UK, 1992) IV , Pitman Research Notes in Math. , 289 , Longman (1993) pp. 126–209 |
| [a23] | M.L. Lapidus, "Analysis on fractals, Laplacians on self-similar sets, noncommutative geometry and spectral dimensions" Topol. Methods in Nonlin. Anal. , 4 (1994) pp. 137–195 |
| [a24] | M.L. Lapidus, "Fractals and vibrations: Can you hear the shape of a fractal drum?" Fractals , 3 (1995) pp. 725–736 (Proc. Symp. Fractal Geometry and Self–Similar Phenomena in honor of Benoit B. Mandelbrot's 70th Birthday (Curaçao, Netherlands Antilles, 1995)) |
| [a25] | M.L. Lapidus, "Towards a noncommutative fractal geometry? Laplacians and volume measures on fractals" Contemp. Math. , 208 (1997) pp. 211–252 |
| [a26] | S.H. Liu, "Fractals and their applications in condensed matter physics" Solid State Phys. , 39 (1986) pp. 207–273 |
| [a27] | B.B. Mandelbrot, "The fractal geometry of nature" , Freeman (1983) (Edition: Revised and enlarged) |
| [a28] | K. Menger, "Allgemeine Räume und Cartesische Räume, Zweite Mitteilung: Über umfassenste  -dimensionale Mengen" Proc. K. Akad. Wetensch. Amsterdam , 29 (1926) pp. 476–482; 1125–1128 (reprinted as Chap. 9 in K. Menger, Dimensionstheorie, Teubner, 1928; English transl.: General spaces and Cartesian spaces, G.A. Edgar (ed.), Classics on fractals, Addison-Wesley, 1993, pp.103-117) -dimensionale Mengen" Proc. K. Akad. Wetensch. Amsterdam , 29 (1926) pp. 476–482; 1125–1128 (reprinted as Chap. 9 in K. Menger, Dimensionstheorie, Teubner, 1928; English transl.: General spaces and Cartesian spaces, G.A. Edgar (ed.), Classics on fractals, Addison-Wesley, 1993, pp.103-117) |
| [a29] | K. Menger, "Dimensionstheorie" , Teubner (1928) |
| [a30] | T. Nakayama, K. Yakubo, R.L. Orbach, "Dynamical properties of fractal networks: Scaling, numerical simulation, and physical realization" Rev. Mod. Phys. , 66 (1994) pp. 381–443 |
| [a31] | E.P.J. Pearse, "Universality of the Sierpiński carpet" Honors Undergraduate Thesis Math. Univ. California , June (1998) (Available from: Univ. Honors Program at UC Riverside and at http://web.dreamsoft.com/freakomatic/sierpinski) |
| [a32] | H.-O. Peitgen, H. Jürgens, D. Saupe, "Chaos and fractals: New frontiers of science" , Springer (1986) |
| [a33] | R. Rammal, "Spectrum of harmonic excitations on fractals" J. Physique , 45 (1984) pp. 191–206 |
| [a34] | R. Rammal, G. Toulouse, "Random walks on fractal structures and percolation clusters" J. Physique Lettres , 44 (1983) pp. L13–L22 |
| [a35] | B. Sapoval, "Les fractales–fractals" , Aditech (1989) |
| [a36] | M.R. Schroeder, "Fractals, chaos, power laws: Minutes from an infinite paradise" , Freeman (1991) |
| [a37] | T. Shima, "On eigenvalue problems for Laplacians on p.c.f. self-similar sets" Japan J. Indus. Appl. Math. , 13 (1996) pp. 1–23 |
| [a38] | W. Sierpiński, "Sur une courbe cantorienne dont tout point est un point de ramification" C.R. Acad. Sci. Paris , 160 (1915) pp. 302 |
| [a39] | W. Sierpiński, "Sur une courbe cantorienne qui contient une image biunivoque et continue de toute courbe donnée" C.R. Acad. Sci. Paris , 162 (1916) pp. 629–632 |
| [a40] | R.S. Strichartz, "Analysis on fractals" Notices Amer. Math. Soc. , 46 (1999) pp. 1199–1208 |
| [a41] | A. Teplyaev, "Spectral analysis on infinite Sierpiński gaskets" J. Funct. Anal. , 159 (1998) pp. 537–567 |
| [a42] | C. Tricot, "Curves and fractal dimensions" , Springer (1995) |
| [a43] | L.M. Blumenthal, K. Menger, "Studies in geometry" , Freeman (1970) |
Sierpinski gasket. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sierpinski_gasket&oldid=23531