Difference between revisions of "Rational surface"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (link) |
||
| Line 1: | Line 1: | ||
A two-dimensional [[Algebraic variety|algebraic variety]], defined over an algebraically closed field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776501.png" />, whose field of rational functions is a purely [[Transcendental extension|transcendental extension]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776502.png" /> of degree 2. Every rational surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776503.png" /> is birationally isomorphic to the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776504.png" />. | A two-dimensional [[Algebraic variety|algebraic variety]], defined over an algebraically closed field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776501.png" />, whose field of rational functions is a purely [[Transcendental extension|transcendental extension]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776502.png" /> of degree 2. Every rational surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776503.png" /> is birationally isomorphic to the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776504.png" />. | ||
| − | The [[Geometric genus|geometric genus]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776505.png" /> and the [[Irregularity|irregularity]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776506.png" /> of a complete smooth rational surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776507.png" /> are equal to 0, that is, there are no regular differential 2- or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776508.png" />-forms on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776509.png" />. Every multiple genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765010.png" /> of a smooth complete rational surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765011.png" /> is also zero, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765012.png" /> is the canonical divisor of the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765013.png" />. These birational invariants distinguish the rational surfaces among all algebraic surfaces, that is, any smooth complete algebraic surface with invariants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765014.png" /> is a rational surface (the Castelnuovo rationality criterion). According to another rationality criterion, a smooth algebraic surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765015.png" /> is a rational surface if and only if there is a non-singular rational curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765016.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765017.png" /> with index of self-intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765018.png" />. | + | The [[Geometric genus|geometric genus]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776505.png" /> and the [[Irregularity|irregularity]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776506.png" /> of a complete smooth rational surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776507.png" /> are equal to 0, that is, there are no regular differential 2- or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776508.png" />-forms on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r0776509.png" />. Every multiple genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765010.png" /> of a smooth complete rational surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765011.png" /> is also zero, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765012.png" /> is the [[canonical divisor]] of the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765013.png" />. These birational invariants distinguish the rational surfaces among all algebraic surfaces, that is, any smooth complete algebraic surface with invariants <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765014.png" /> is a rational surface (the Castelnuovo rationality criterion). According to another rationality criterion, a smooth algebraic surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765015.png" /> is a rational surface if and only if there is a non-singular rational curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765016.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765017.png" /> with index of self-intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765018.png" />. |
With the exception of rational surfaces and ruled surfaces, every algebraic surface is birationally isomorphic to a unique minimal model. In the class of rational surfaces there is a countable set of minimal models. It consists of the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765019.png" /> and the surfaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765020.png" /> (projectivization of two-dimensional vector bundles over the projective line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765021.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765022.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765024.png" />. In other words, the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765025.png" /> is a fibration by rational curves over a rational curve with a section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765026.png" /> which is a smooth rational curve with index of self-intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765027.png" />. The surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765028.png" /> is isomorphic to the direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765029.png" />, and the surfaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765030.png" /> are obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765031.png" /> by a sequence of elementary transformations (see [[#References|[1]]]). | With the exception of rational surfaces and ruled surfaces, every algebraic surface is birationally isomorphic to a unique minimal model. In the class of rational surfaces there is a countable set of minimal models. It consists of the projective space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765019.png" /> and the surfaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765020.png" /> (projectivization of two-dimensional vector bundles over the projective line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765021.png" />), <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765022.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765024.png" />. In other words, the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765025.png" /> is a fibration by rational curves over a rational curve with a section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765026.png" /> which is a smooth rational curve with index of self-intersection <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765027.png" />. The surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765028.png" /> is isomorphic to the direct product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765029.png" />, and the surfaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765030.png" /> are obtained from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077650/r07765031.png" /> by a sequence of elementary transformations (see [[#References|[1]]]). | ||
Revision as of 18:21, 19 October 2017
A two-dimensional algebraic variety, defined over an algebraically closed field  , whose field of rational functions is a purely transcendental extension of
, whose field of rational functions is a purely transcendental extension of 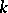 of degree 2. Every rational surface
of degree 2. Every rational surface 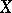 is birationally isomorphic to the projective space
is birationally isomorphic to the projective space 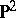 .
.
The geometric genus  and the irregularity
and the irregularity  of a complete smooth rational surface
of a complete smooth rational surface  are equal to 0, that is, there are no regular differential 2- or
are equal to 0, that is, there are no regular differential 2- or 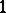 -forms on
-forms on 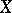 . Every multiple genus
. Every multiple genus  of a smooth complete rational surface
of a smooth complete rational surface 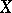 is also zero, where
is also zero, where 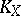 is the canonical divisor of the surface
is the canonical divisor of the surface 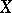 . These birational invariants distinguish the rational surfaces among all algebraic surfaces, that is, any smooth complete algebraic surface with invariants
. These birational invariants distinguish the rational surfaces among all algebraic surfaces, that is, any smooth complete algebraic surface with invariants 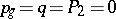 is a rational surface (the Castelnuovo rationality criterion). According to another rationality criterion, a smooth algebraic surface
is a rational surface (the Castelnuovo rationality criterion). According to another rationality criterion, a smooth algebraic surface  is a rational surface if and only if there is a non-singular rational curve
is a rational surface if and only if there is a non-singular rational curve 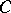 on
on 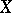 with index of self-intersection
with index of self-intersection 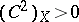 .
.
With the exception of rational surfaces and ruled surfaces, every algebraic surface is birationally isomorphic to a unique minimal model. In the class of rational surfaces there is a countable set of minimal models. It consists of the projective space 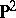 and the surfaces
and the surfaces 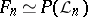 (projectivization of two-dimensional vector bundles over the projective line
(projectivization of two-dimensional vector bundles over the projective line 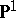 ),
), 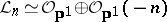 , where
, where 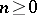 and
and 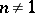 . In other words, the surface
. In other words, the surface 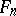 is a fibration by rational curves over a rational curve with a section
is a fibration by rational curves over a rational curve with a section 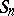 which is a smooth rational curve with index of self-intersection
which is a smooth rational curve with index of self-intersection  . The surface
. The surface 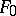 is isomorphic to the direct product
is isomorphic to the direct product 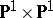 , and the surfaces
, and the surfaces 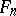 are obtained from
are obtained from 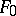 by a sequence of elementary transformations (see [1]).
by a sequence of elementary transformations (see [1]).
Rational surfaces have a large group of birational transformations (called the group of Cremona transformations).
If the anti-canonical sheaf 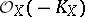 on a smooth complete rational surface is ample (cf. Ample sheaf), then
on a smooth complete rational surface is ample (cf. Ample sheaf), then 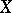 is called a Del Pezzo surface. The greatest integer
is called a Del Pezzo surface. The greatest integer 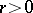 such that
such that 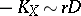 for some divisor
for some divisor 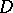 on
on  is called the index of the Del Pezzo surface. The index
is called the index of the Del Pezzo surface. The index  is equal to 1, 2 or 3 (see [2]). A Del Pezzo surface of index 3 is isomorphic to
is equal to 1, 2 or 3 (see [2]). A Del Pezzo surface of index 3 is isomorphic to 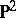 . For a Del Pezzo surface
. For a Del Pezzo surface 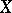 of index 2, the rational mapping
of index 2, the rational mapping 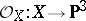 defined by the sheaf
defined by the sheaf 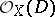 gives a birational isomorphism onto a quadric in
gives a birational isomorphism onto a quadric in 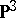 . Del Pezzo surfaces of index 1 can be obtained by
. Del Pezzo surfaces of index 1 can be obtained by  monoidal transformations (cf. Monoidal transformation) of the plane
monoidal transformations (cf. Monoidal transformation) of the plane 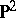 with centres at points in general position, where
with centres at points in general position, where 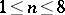 (see [2]).
(see [2]).
References
| [1] | I.R. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001 |
| [2] | V.A. Iskovskii, "Anticanonical models of three-dimensional algebraic varieties" , Current problems in mathematics , 12 , Moscow (1979) pp. 59–157; 239 (In Russian) |
| [3] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
Comments
If 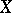 is defined over a, not necessarily algebraically closed, field and
is defined over a, not necessarily algebraically closed, field and 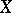 is birationally equivalent to
is birationally equivalent to 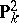 over
over 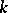 , then
, then 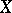 is said to be a
is said to be a 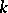 -rational surface.
-rational surface.
References
| [a1] | A. Beauville, "Surfaces algébriques complexes" Astérisque , 54 (1978) MR0485887 Zbl 0394.14014 |
| [a2] | J. Semple, L. Roth, "Introduction to algebraic geometry" , Oxford Univ. Press (1985) MR0814690 Zbl 0576.14001 |
Rational surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rational_surface&oldid=23951