Difference between revisions of "Kodaira dimension"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Algebraic surfaces" ''Proc. Steklov Inst. Math.'' , '''75''' (1967) ''Trudy Mat. Inst. Steklov.'' , '''75''' (1965) {{MR|1392959}} {{MR|1060325}} {{ZBL|0830.00008}} {{ZBL|0733.14015}} {{ZBL|0832.14026}} {{ZBL|0509.14036}} {{ZBL|0492.14024}} {{ZBL|0379.14006}} {{ZBL|0253.14006}} {{ZBL|0154.21001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K. Ueno, "Classification theory of algebraic varieties and compact complex spaces" , Springer (1975) {{MR|0506253}} {{ZBL|0299.14007}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Iitaka, "On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/k/k055/k055630/k05563028.png" />-dimensions of algebraic varieties" ''J. Math. Soc. Japan'' , '''23''' (1971) pp. 356–373 {{MR|285531}} {{ZBL|}} </TD></TR></table> |
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. van de Ven, "Compact complex surfaces" , Springer (1984) {{MR|}} {{ZBL|0718.14023}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S. Iitaka, "Algebraic geometry, an introduction to birational geometry of algebraic varieties" , Springer (1982) pp. Chapt. 10 {{MR|}} {{ZBL|0491.14006}} </TD></TR></table> |
Revision as of 21:53, 30 March 2012
A numerical invariant of an algebraic variety, named after K. Kodaira who first pointed out the importance of this invariant in the theory of the classification of algebraic varieties.
Let  be a non-singular algebraic variety and let
be a non-singular algebraic variety and let  be a rational mapping defined by a linear system
be a rational mapping defined by a linear system  , where
, where  is the canonical class of
is the canonical class of  . The Kodaira dimension
. The Kodaira dimension  of
of  is defined as
is defined as  . Here, if
. Here, if  for all
for all  , then it is assumed that
, then it is assumed that 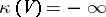 . The Kodaira dimension is a birational invariant, that is, it does not depend on the representative in the birational equivalence class.
. The Kodaira dimension is a birational invariant, that is, it does not depend on the representative in the birational equivalence class.
Suppose that the ground field is the field of the complex numbers 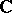 . If
. If 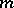 is sufficiently large, then one has the estimate
is sufficiently large, then one has the estimate
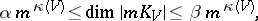 |
where 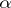 ,
,  are certain positive numbers. If
are certain positive numbers. If  , then there exists a surjective morphism
, then there exists a surjective morphism 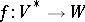 of algebraic varieties such that: a)
of algebraic varieties such that: a) 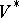 is birationally equivalent to
is birationally equivalent to 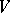 ; b)
; b) 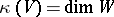 ; and c) for some dense open set
; and c) for some dense open set 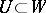 , all the fibres
, all the fibres 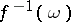 ,
, 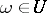 , are varieties of parabolic type (i.e. of Kodaira dimension zero).
, are varieties of parabolic type (i.e. of Kodaira dimension zero).
There is a generalization of the notion of the Kodaira dimension (see [2]) to the case when in the linear system 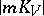 the canonical class
the canonical class 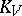 is replaced by an arbitrary divisor
is replaced by an arbitrary divisor 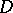 .
.
References
| [1] | I.R. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001 |
| [2] | K. Ueno, "Classification theory of algebraic varieties and compact complex spaces" , Springer (1975) MR0506253 Zbl 0299.14007 |
| [3] | S. Iitaka, "On 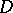 -dimensions of algebraic varieties" J. Math. Soc. Japan , 23 (1971) pp. 356–373 MR285531 -dimensions of algebraic varieties" J. Math. Soc. Japan , 23 (1971) pp. 356–373 MR285531 |
Comments
Let 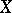 be a compact connected complex manifold. Let
be a compact connected complex manifold. Let 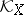 be the canonical bundle on
be the canonical bundle on  . There is a canonical pairing of sections
. There is a canonical pairing of sections
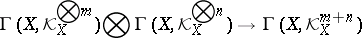 |
making 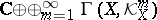 into a commutative ring
into a commutative ring 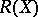 , called the canonical ring of
, called the canonical ring of 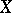 . It can be proved to be of finite transcendence degree,
. It can be proved to be of finite transcendence degree, 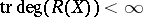 . The Kodaira dimension of
. The Kodaira dimension of  is now described as follows:
is now described as follows:
 |
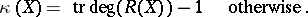 |
It is always true that 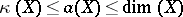 , where
, where 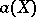 is the algebraic dimension of
is the algebraic dimension of 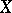 , i.e. the transcendence degree of the field of meromorphic functions on
, i.e. the transcendence degree of the field of meromorphic functions on  . Let
. Let 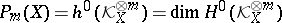 be the
be the 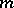 -th plurigenus of
-th plurigenus of 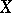 . Then one has: i)
. Then one has: i)  if and only if
if and only if  for all
for all 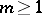 ; ii)
; ii)  if and only if
if and only if 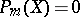 or 1 for
or 1 for  , but not always 0; iii)
, but not always 0; iii) 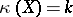 , with
, with  , if and only if
, if and only if 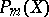 has growth
has growth 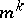 , i.e. if and only if there exists an integer
, i.e. if and only if there exists an integer 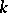 and strictly positive constants
and strictly positive constants  ,
, 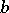 such that
such that  for large
for large 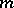 .
.
The Kodaira dimension is also called the canonical dimension. For the concept of the logarithmic Kodaira dimension see [a2], Chapt. 11.
References
| [a1] | A. van de Ven, "Compact complex surfaces" , Springer (1984) Zbl 0718.14023 |
| [a2] | S. Iitaka, "Algebraic geometry, an introduction to birational geometry of algebraic varieties" , Springer (1982) pp. Chapt. 10 Zbl 0491.14006 |
Kodaira dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kodaira_dimension&oldid=13517