Federer-Fleming deformation theorem
The Federer–Fleming deformation theorem can be considered as one of the central results in the theory of integral currents, created by H. Federer and W.H. Fleming at the end of 1950s, [a1]. The notion of an integral current was introduced to meet all the requirements of the concept of "k-dimensional domain of integration in Euclidean n-space" and combines the smoothness properties of differentiable manifolds and the combinatorial structure of polyhedral chains with integer coefficients. The notion of integral current provides a powerful instrument for solving geometrical variational problems like the Plateau problem.
The deformation theorem shows how one can deform normal and integral currents into similar currents with supports in the appropriate skeletons of a standard cubical cell complex with given cube edge, and gives estimates for the masses of the currents.
Let 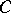 denote the standard cubical complex in the Euclidean space
denote the standard cubical complex in the Euclidean space 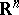 generated by the cubes with edge
generated by the cubes with edge  and with centres at the integer points. Let
and with centres at the integer points. Let 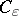 denote the complex obtained from
denote the complex obtained from 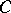 by
by  -homothety (cf. Homothety). As always, let
-homothety (cf. Homothety). As always, let 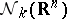 denote the space of normal currents in
denote the space of normal currents in 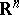 , and let
, and let 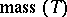 be the mass of the current
be the mass of the current 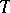 (cf. also Differential form; Mass and co-mass).
(cf. also Differential form; Mass and co-mass).
The Federer–Fleming deformation theorem reads: Let 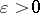 be an arbitrary positive number. Then any
be an arbitrary positive number. Then any  -dimensional normal current
-dimensional normal current  in
in 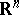 can be represented as a sum
can be represented as a sum
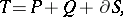 |
where
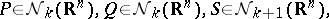 |
with the following properties:
1) The current  is a polyhedral chain of
is a polyhedral chain of 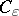 with real coefficients. If
with real coefficients. If  is an integral current, then the coefficients of
is an integral current, then the coefficients of 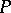 are integers.
are integers.
2) The supports of 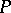 and
and 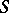 lie in the
lie in the  -neighbourhood of the support of
-neighbourhood of the support of 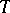 , and the supports of
, and the supports of 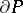 and
and  lie in the
lie in the  -neighbourhood of
-neighbourhood of 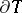 .
.
3) For the masses of 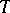 ,
, 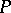 ,
, 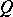 , and
, and 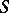 the following estimates hold:
the following estimates hold:
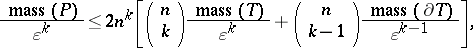 |
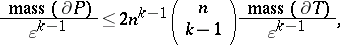 |
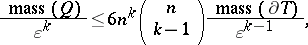 |
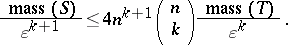 |
4) If 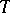 is an integral current, then so are
is an integral current, then so are 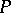 ,
,  and
and 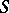 .
.
5) If 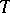 is an (integral) Lipschitz chain, so are
is an (integral) Lipschitz chain, so are 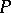 ,
, 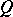 and
and 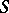 .
.
6) If  is an (integral) Lipschitz chain, so is
is an (integral) Lipschitz chain, so is 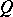 .
.
As a consequence, one can obtain the following result: For each integral current  there exists a sequence of integral Lipschitz chains
there exists a sequence of integral Lipschitz chains 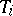 such that
such that
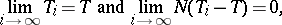 |
where  .
.
As other applications of the theorem, one can obtain the theorem about isomorphism between the integer singular homology groups of  and the homology groups of the integral current chain complex
and the homology groups of the integral current chain complex 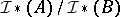 , where
, where 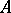 and
and 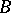 are local Lipschitz neighbourhood retracts in
are local Lipschitz neighbourhood retracts in 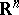 ; the isoperimetric inequalities for integral currents; etc. Some modern applications of the theorem can be found in [a2], [a3].
; the isoperimetric inequalities for integral currents; etc. Some modern applications of the theorem can be found in [a2], [a3].
References
| [a1] | H. Federer, W.H. Fleming, "Normal and integral currents" Ann. of Math. , 72 : 3 (1960) pp. 458–520 MR0123260 Zbl 0187.31301 |
| [a2] | Dao Trong Thi, A.T. Fomenko, "Minimal surfaces, stratified multivarifolds and the Plateau problem" , Amer. Math. Soc. (1991) |
| [a3] | A.T. Fomenko, "Variational principles in topology: multidimensional minimal surface theory" , Kluwer Acad. Publ. (1990) |
Federer-Fleming deformation theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Federer-Fleming_deformation_theorem&oldid=28190