Euler identity
The relation
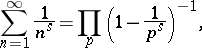 |
where 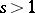 is an arbitrary real number and the product extends over all prime numbers
is an arbitrary real number and the product extends over all prime numbers 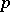 . The Euler identity also holds for all complex numbers
. The Euler identity also holds for all complex numbers 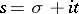 with
with 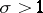 .
.
The Euler identity can be generalized in the form
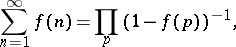 |
which holds for every totally-multiplicative arithmetic function 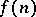 for which the series
for which the series 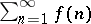 is absolutely convergent.
is absolutely convergent.
Another generalization of the Euler identity is the formula
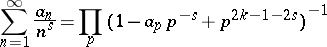 |
for the Dirichlet series
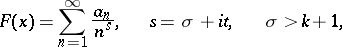 |
corresponding to the modular functions
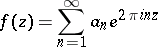 |
of weight 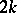 , which are the eigen functions of the Hecke operator.
, which are the eigen functions of the Hecke operator.
References
| [1] | K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968) |
| [2] | S. Lang, "Introduction to modular forms" , Springer (1976) |
Comments
The product
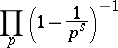 |
is called the Euler product. For Hecke operators in connection with modular forms see Modular form. For totally-multiplicative arithmetic functions cf. Multiplicative arithmetic function.
References
| [a1] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) |
Euler identity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_identity&oldid=11612