Contravariant tensor
of valency 
A tensor of type  , i.e. an element of the tensor product
, i.e. an element of the tensor product
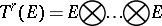 |
of  copies of a vector space
copies of a vector space  over a field
over a field  . The space
. The space  is a vector space over
is a vector space over  with respect to the operations of addition of contravariant tensors of the same valency and multiplication of them by a scalar. Let
with respect to the operations of addition of contravariant tensors of the same valency and multiplication of them by a scalar. Let  be a finite-dimensional vector space with basis
be a finite-dimensional vector space with basis  . Then the dimension of
. Then the dimension of  is
is 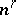 ; one possible basis in
; one possible basis in  is given by all possible contravariant tensors of the form
is given by all possible contravariant tensors of the form
 |
Any contravariant tensor  can be represented in the form
can be represented in the form
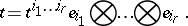 |
The numbers 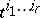 are called the coordinates or components of
are called the coordinates or components of 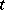 with respect to
with respect to  in
in  . On changing to a new basis in
. On changing to a new basis in  according to the formulas
according to the formulas
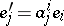 |
the components of  change according to the so-called contravariant law
change according to the so-called contravariant law
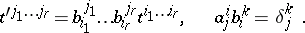 |
When the valency  equals 1, a contravariant tensor is the same as a vector, that is, an element of
equals 1, a contravariant tensor is the same as a vector, that is, an element of 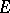 ; when
; when  , a contravariant tensor can be related in an invariant way with an
, a contravariant tensor can be related in an invariant way with an  -linear mapping into
-linear mapping into  of the direct product
of the direct product
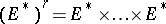 |
of  copies of the dual space
copies of the dual space  to
to 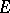 . For this it suffices to take as the components of the contravariant tensor
. For this it suffices to take as the components of the contravariant tensor 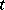 the values of the
the values of the  -linear mapping
-linear mapping  at
at  (where
(where 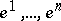 are the basis elements in
are the basis elements in 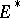 dual to
dual to  , that is,
, that is, 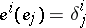 ), and conversely. For this reason contravariant tensors are sometimes directly defined as multilinear functionals on
), and conversely. For this reason contravariant tensors are sometimes directly defined as multilinear functionals on 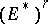 .
.
Comments
More generally, let 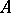 be a commutative ring with unit element and
be a commutative ring with unit element and  a unitary module over
a unitary module over 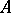 . Then the elements of the
. Then the elements of the  -fold tensor product
-fold tensor product 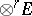 are called
are called  -contravariant tensors or contravariant tensors of valency or order
-contravariant tensors or contravariant tensors of valency or order  . The phrase "contravariant tensor of order r" is also used to denote a contravariant tensor field of order
. The phrase "contravariant tensor of order r" is also used to denote a contravariant tensor field of order  over a smooth manifold
over a smooth manifold  ; cf. Tensor bundle. Such a field assigns to each
; cf. Tensor bundle. Such a field assigns to each 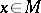 an element of
an element of  , the
, the  -fold tensor product of the tangent space to
-fold tensor product of the tangent space to  at
at  . In the setting of rings and modules such a tensor field is simply an
. In the setting of rings and modules such a tensor field is simply an  -contravariant tensor of the module
-contravariant tensor of the module 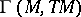 of sections of
of sections of 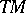 (i.e. the vector fields) over the ring
(i.e. the vector fields) over the ring  of smooth functions on
of smooth functions on 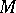 .
.
References
| [a1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Multilinear algebra" , Addison-Wesley (1974) pp. Chapt. 3 (Translated from French) |
| [a2] | M. Marcus, "Finite dimensional multilinear algebra" , 1 , M. Dekker (1973) |
| [a3] | B. Spain, "Tensor calculus" , Oliver & Boyd (1970) |
Contravariant tensor. I.Kh. Sabitov (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contravariant_tensor&oldid=19302