Carathéodory theorem
on conformal mapping of domains with variable boundaries
One of the main results in the theory of conformal mapping of domains with variable boundaries; obtained by C. Carathéodory [1].
Let 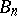 ,
, 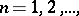 be a sequence of simply-connected domains of the
be a sequence of simply-connected domains of the  -plane containing a fixed point
-plane containing a fixed point 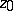 ,
, 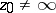 . If there exists a disc
. If there exists a disc 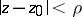 ,
, 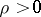 , belonging to all
, belonging to all  , then the kernel of the sequence
, then the kernel of the sequence 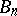 ,
, 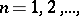 with respect to
with respect to  is the largest domain
is the largest domain 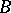 containing
containing 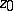 and such that for each compact set
and such that for each compact set 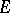 belonging to
belonging to  there is an
there is an 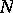 such that
such that 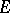 belongs to
belongs to 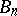 for all
for all 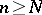 . A largest domain is one which contains any other domain having the same property. If there is no such a disc, then by the kernel
. A largest domain is one which contains any other domain having the same property. If there is no such a disc, then by the kernel 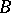 of the sequence
of the sequence 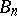 ,
, 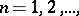 one means the point
one means the point 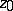 (in this case one says that the sequence
(in this case one says that the sequence 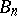 ,
, 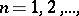 has a degenerate kernel). A sequence of domains
has a degenerate kernel). A sequence of domains 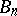 ,
,  converges to a kernel
converges to a kernel 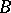 if any subsequence of
if any subsequence of  has
has  as its kernel.
as its kernel.
Carathéodory's theorem. Suppose that one is given a sequence of functions 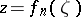 ,
,  ,
, 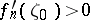 ,
, 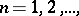 that are regular and univalent in the disc
that are regular and univalent in the disc 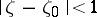 and that map this disc onto the domains
and that map this disc onto the domains 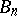 , respectively. Then in order that the sequence
, respectively. Then in order that the sequence 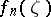 ,
,  converges in the disc
converges in the disc  to a finite function
to a finite function 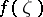 , it is necessary and sufficient that the sequence
, it is necessary and sufficient that the sequence 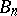 ,
, 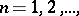 converges to a kernel
converges to a kernel 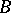 which is either the point
which is either the point 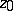 or a domain containing more than one boundary point. Moreover, the convergence is uniform on compact sets in the interior of the disc
or a domain containing more than one boundary point. Moreover, the convergence is uniform on compact sets in the interior of the disc 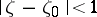 . If the limit function
. If the limit function  , then it maps the disc
, then it maps the disc 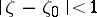 univalently onto
univalently onto 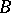 , and the inverse functions
, and the inverse functions 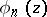 ,
,  are uniformly convergent on compact sets in the interior of
are uniformly convergent on compact sets in the interior of 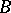 to the inverse function
to the inverse function 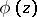 of
of 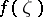 .
.
The question of the convergence of univalent functions in multiply-connected domains is considered analogously. One such theorem is given below for unbounded domains. Let 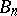 ,
, 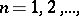 be a sequence of domains in the
be a sequence of domains in the  -plane containing some fixed neighbourhood of
-plane containing some fixed neighbourhood of 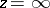 . Then the kernel of the sequence
. Then the kernel of the sequence 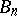 ,
,  with respect to
with respect to 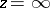 is the largest domain
is the largest domain 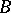 containing
containing 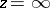 and such that any closed subdomain of it is a subset of all
and such that any closed subdomain of it is a subset of all 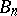 from some
from some  onwards. Convergence of the sequence
onwards. Convergence of the sequence 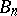 ,
, 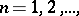 to the kernel
to the kernel 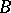 is defined as before. The following theorem holds [2]. Let
is defined as before. The following theorem holds [2]. Let 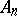 ,
, 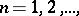 be a sequence of domains in the
be a sequence of domains in the  -plane containing
-plane containing 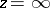 and converging to a kernel
and converging to a kernel 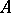 , and suppose that the functions
, and suppose that the functions 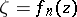 ,
, 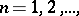 map them univalently onto corresponding domains
map them univalently onto corresponding domains 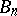 containing
containing 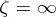 ;
; 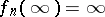 ,
, 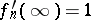 ,
, 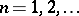 . Then in order that the sequence
. Then in order that the sequence  ,
, 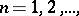 converges uniformly on compact sets in the interior of
converges uniformly on compact sets in the interior of 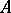 to a univalent function
to a univalent function 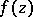 , it is necessary and sufficient that the sequence
, it is necessary and sufficient that the sequence 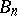 ,
, 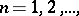 possesses a kernel
possesses a kernel 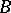 and converges to it. In this case
and converges to it. In this case 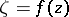 maps
maps 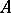 univalently onto
univalently onto 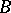 .
.
It is possible to give other theorems on the convergence of a sequence of univalent functions, in dependence of the method of normalizing them (see [2]).
References
| [1] | C. Carathéodory, "Untersuchungen über die konformen Abbildungen von festen und veränderlichen Gebieten" Math. Ann. , 72 (1912) pp. 107–144 |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Chapt. 3 |
Carathéodory theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory_theorem&oldid=43541