Difference between revisions of "Aleph"
(Importing text file) |
m (links) |
||
| Line 1: | Line 1: | ||
''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112702.png" />'' | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112702.png" />'' | ||
| − | The first letter of the Hebrew alphabet. As symbols alephs were introduced by G. Cantor to denote the cardinal numbers (the cardinality cf. [[Cardinal number|Cardinal number]]) of infinite well-ordered sets. Each cardinal number is some aleph (a consequence of the [[Axiom of choice|axiom of choice]]). However, many theorems about alephs are demonstrated without recourse to the axiom of choice. For each ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112703.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112704.png" /> one denotes the cardinality of the set of all ordinal numbers smaller than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112705.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112706.png" /> is the cardinality of the set of all natural numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112707.png" /> is the cardinality of the set of all countable ordinal numbers, etc. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112708.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112709.png" />. The cardinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127010.png" /> is the smallest cardinal number which follows <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127011.png" />. The generalized continuum hypothesis states that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127012.png" /> for any ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127013.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127014.png" />, the equation assumes the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127015.png" />, and forms the content of the [[Continuum hypothesis|continuum hypothesis]]. The set of all alephs smaller than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127016.png" /> is totally ordered according to magnitude, and its [[ | + | The first letter of the Hebrew alphabet. As symbols alephs were introduced by G. Cantor to denote the cardinal numbers (the cardinality cf. [[Cardinal number|Cardinal number]]) of infinite well-ordered sets. Each cardinal number is some aleph (a consequence of the [[Axiom of choice|axiom of choice]]). However, many theorems about alephs are demonstrated without recourse to the axiom of choice. For each ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112703.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112704.png" /> one denotes the cardinality of the set of all ordinal numbers smaller than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112705.png" />. In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112706.png" /> is the cardinality of the set of all natural numbers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112707.png" /> is the cardinality of the set of all countable ordinal numbers, etc. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112708.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a0112709.png" />. The cardinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127010.png" /> is the smallest cardinal number which follows <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127011.png" />. The generalized continuum hypothesis states that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127012.png" /> for any ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127013.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127014.png" />, the equation assumes the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127015.png" />, and forms the content of the [[Continuum hypothesis|continuum hypothesis]]. The set of all alephs smaller than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127016.png" /> is totally ordered according to magnitude, and its [[order type]] is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127017.png" />. The definitions of the sum, the product and a power of alephs are obvious. One has |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127018.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127018.png" /></td> </tr></table> | ||
| Line 13: | Line 13: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127021.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127021.png" /></td> </tr></table> | ||
| − | The recursive formula of Tarski: If an ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127022.png" /> is a limit ordinal, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127023.png" />, then | + | The recursive formula of Tarski: If an ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127022.png" /> is a [[limit ordinal]], and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127023.png" />, then |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127024.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127024.png" /></td> </tr></table> | ||
| − | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127025.png" /> denotes the | + | Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127025.png" /> denotes the cofinal character of the ordinal number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127026.png" />. As in the case of cardinal numbers, one distinguishes between singular alephs, regular alephs, limit alephs, weakly inaccessible alephs, strongly inaccessible alephs, etc. For example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127027.png" /> is singular if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127028.png" /> is a limit ordinal and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011270/a01127029.png" />. There is no largest aleph among all alephs. It was shown by Cantor that the set of all alephs is meaningless, i.e. that there is no such set. See also [[Totally well-ordered set|Totally well-ordered set]]; [[Continuum hypothesis|Continuum hypothesis]]; [[Set theory|Set theory]]; [[Ordinal number|Ordinal number]]; [[Cardinal number|Cardinal number]]. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.J. Cohen, "Set theory and the continuum hypothesis" , Benjamin (1966)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> P.J. Cohen, "Set theory and the continuum hypothesis" , Benjamin (1966)</TD></TR> | ||
| + | <TR><TD valign="top">[4]</TD> <TD valign="top"> K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968)</TD></TR> | ||
| + | </table> | ||
| Line 36: | Line 41: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Levy, "Basic set theory" , Springer (1979)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Silver, "On the singular cardinals problem" R. James (ed.) , ''Proc. Internat. Congress Mathematicians (Vancouver, 1974)'' , '''1''' , Canad. Math. Congress (1975) pp. 265–268</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Levy, "Basic set theory" , Springer (1979)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Silver, "On the singular cardinals problem" R. James (ed.) , ''Proc. Internat. Congress Mathematicians (Vancouver, 1974)'' , '''1''' , Canad. Math. Congress (1975) pp. 265–268</TD></TR> | ||
| + | </table> | ||
Revision as of 07:37, 27 November 2014
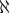
The first letter of the Hebrew alphabet. As symbols alephs were introduced by G. Cantor to denote the cardinal numbers (the cardinality cf. Cardinal number) of infinite well-ordered sets. Each cardinal number is some aleph (a consequence of the axiom of choice). However, many theorems about alephs are demonstrated without recourse to the axiom of choice. For each ordinal number  by
by 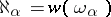 one denotes the cardinality of the set of all ordinal numbers smaller than
one denotes the cardinality of the set of all ordinal numbers smaller than 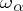 . In particular,
. In particular, 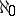 is the cardinality of the set of all natural numbers,
is the cardinality of the set of all natural numbers, 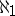 is the cardinality of the set of all countable ordinal numbers, etc. If
is the cardinality of the set of all countable ordinal numbers, etc. If 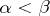 , then
, then 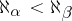 . The cardinal number
. The cardinal number 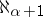 is the smallest cardinal number which follows
is the smallest cardinal number which follows 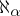 . The generalized continuum hypothesis states that
. The generalized continuum hypothesis states that 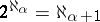 for any ordinal number
for any ordinal number 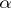 . If
. If 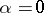 , the equation assumes the form
, the equation assumes the form 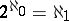 , and forms the content of the continuum hypothesis. The set of all alephs smaller than
, and forms the content of the continuum hypothesis. The set of all alephs smaller than 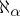 is totally ordered according to magnitude, and its order type is
is totally ordered according to magnitude, and its order type is 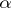 . The definitions of the sum, the product and a power of alephs are obvious. One has
. The definitions of the sum, the product and a power of alephs are obvious. One has
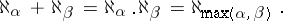 |
The following formulas are most-frequently encountered. The recursive Hausdorff formula:
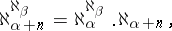 |
a particular case of which, for 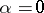 , is the Bernshtein formula:
, is the Bernshtein formula:
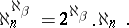 |
The recursive formula of Tarski: If an ordinal number 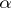 is a limit ordinal, and if
is a limit ordinal, and if 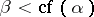 , then
, then
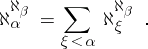 |
Here 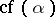 denotes the cofinal character of the ordinal number
denotes the cofinal character of the ordinal number 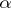 . As in the case of cardinal numbers, one distinguishes between singular alephs, regular alephs, limit alephs, weakly inaccessible alephs, strongly inaccessible alephs, etc. For example,
. As in the case of cardinal numbers, one distinguishes between singular alephs, regular alephs, limit alephs, weakly inaccessible alephs, strongly inaccessible alephs, etc. For example, 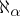 is singular if
is singular if 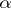 is a limit ordinal and if
is a limit ordinal and if 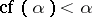 . There is no largest aleph among all alephs. It was shown by Cantor that the set of all alephs is meaningless, i.e. that there is no such set. See also Totally well-ordered set; Continuum hypothesis; Set theory; Ordinal number; Cardinal number.
. There is no largest aleph among all alephs. It was shown by Cantor that the set of all alephs is meaningless, i.e. that there is no such set. See also Totally well-ordered set; Continuum hypothesis; Set theory; Ordinal number; Cardinal number.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die Theorie der reellen Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [2] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [3] | P.J. Cohen, "Set theory and the continuum hypothesis" , Benjamin (1966) |
| [4] | K. Kuratowski, A. Mostowski, "Set theory" , North-Holland (1968) |
Comments
A more recent theorem on the exponentiation of alephs was proved by J. Silver in 1974, cf. [a2]. A particular case says that if
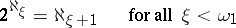 |
then
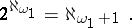 |
A reasonable up-to-date additional reference for this topic is [a1].
References
| [a1] | A. Levy, "Basic set theory" , Springer (1979) |
| [a2] | J. Silver, "On the singular cardinals problem" R. James (ed.) , Proc. Internat. Congress Mathematicians (Vancouver, 1974) , 1 , Canad. Math. Congress (1975) pp. 265–268 |
Aleph. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Aleph&oldid=18544