Extension of a module
Any module  containing the given module
containing the given module  as a submodule. Usually one fixes a quotient module
as a submodule. Usually one fixes a quotient module  , that is, an extension of the module
, that is, an extension of the module  by the module
by the module  is an exact sequence
is an exact sequence
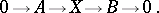 |
Such a module  always exists (for example, the direct sum of
always exists (for example, the direct sum of  and
and 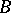 ), but need not be uniquely determined by
), but need not be uniquely determined by 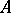 and
and  . Both in the theory of modules and in its applications there is a need to describe all different extensions of a module
. Both in the theory of modules and in its applications there is a need to describe all different extensions of a module 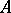 by a module
by a module 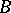 . To this end one defines an equivalence relation on the class of all extensions of
. To this end one defines an equivalence relation on the class of all extensions of 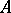 by
by 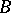 as well as a binary operation (called Baer multiplication) on the set of equivalence classes, which thus becomes an Abelian group
as well as a binary operation (called Baer multiplication) on the set of equivalence classes, which thus becomes an Abelian group 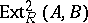 , where
, where 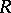 is the ring over which
is the ring over which 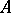 is a module. This construction can be extended to
is a module. This construction can be extended to  -fold extensions of
-fold extensions of 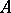 by
by 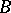 , i.e. to exact sequences of the form
, i.e. to exact sequences of the form
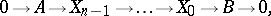 |
corresponding to the group 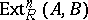 . The groups
. The groups
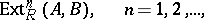 |
are the derived functors of the functor 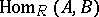 , and may be computed using a projective resolution of
, and may be computed using a projective resolution of  or an injective resolution of
or an injective resolution of 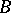 . An extension
. An extension 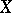 of
of  is called essential if
is called essential if 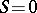 is the only submodule of
is the only submodule of  with
with  . Every module has a maximal essential extension and this is the minimal injective module containing the given one.
. Every module has a maximal essential extension and this is the minimal injective module containing the given one.
For references see Extension of a group.
Comments
The minimal injective module containing 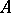 is called the injective hull or envelope of
is called the injective hull or envelope of  . The notion can be defined in any Abelian category, cf. [a1]. The dual notion is that of a projective covering.
. The notion can be defined in any Abelian category, cf. [a1]. The dual notion is that of a projective covering.
References
| [a1] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
Extension of a module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_of_a_module&oldid=39561