Local dimension
of a normal topological space 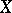
The topological invariant 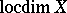 , defined as follows. One says that
, defined as follows. One says that  ,
,  if for any point
if for any point 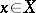 there is a neighbourhood
there is a neighbourhood  for which the Lebesgue dimension of its closure satisfies the relation
for which the Lebesgue dimension of its closure satisfies the relation 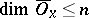 . If
. If  for some
for some  , then the local dimension of
, then the local dimension of 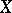 is finite, so one writes
is finite, so one writes 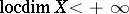 and puts
and puts
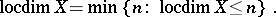 |
Always 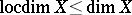 ; there are normal spaces
; there are normal spaces 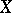 with
with 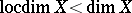 ; in the class of paracompact spaces always
; in the class of paracompact spaces always  . If in the definition of local dimension the Lebesgue dimension
. If in the definition of local dimension the Lebesgue dimension 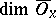 is replaced by the large inductive dimension
is replaced by the large inductive dimension 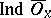 , then one obtains the definition of the local large inductive dimension
, then one obtains the definition of the local large inductive dimension 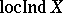 .
.
Comments
See [a1] for a construction of a space with 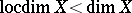 and — as an application — a hereditarily normal space
and — as an application — a hereditarily normal space  with
with 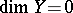 yet
yet 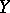 contains subspaces of arbitrary high dimension.
contains subspaces of arbitrary high dimension.
For the notions of the local dimension at a point of an analytic space, algebraic variety or scheme cf. Analytic space; Dimension of an associative ring; Analytic set, and Spectrum of a ring.
References
| [a1] | E. Pol, R. Pol, "A hereditarily normal strongly zero-dimensional space containing subspaces of arbitrarily large dimension" Fund. Math. , 102 (1979) pp. 137–142 |
| [a2] | R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50 |
Local dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_dimension&oldid=33942