Mixed integral equation
An integral equation that, in the one-dimensional case, has the form
 | (1) |
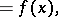 |
where 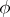 is the unknown and
is the unknown and 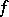 is a given continuous function on
is a given continuous function on 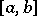 ,
,  ,
, 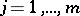 , are given points, and
, are given points, and 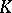 ,
, 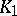 are given continuous functions on the rectangle
are given continuous functions on the rectangle 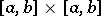 . If
. If
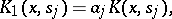 |
where the 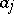 are positive constants, then (1) can be written as
are positive constants, then (1) can be written as
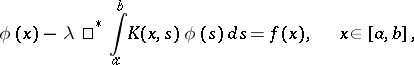 | (2) |
where the new integration symbol, with 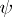 an arbitrary finite integrable function, is defined by (see [1]):
an arbitrary finite integrable function, is defined by (see [1]):
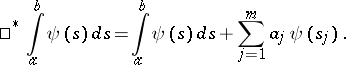 |
The theory of Fredholm equations (cf. Fredholm equation) and, in the case of a symmetric kernel, the theory of integral equations with symmetric kernel (cf. Integral equation with symmetric kernel), is valid for equation (2).
In the case of multi-dimensional mixed integral equations, the unknown function can be part of the integrands of integrals over manifolds of different dimensions. For example, in the two-dimensional case the integral equation may have the form
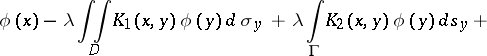 |
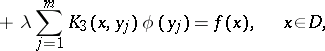 |
where 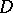 is some domain in the plane,
is some domain in the plane, 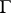 is its boundary, and
is its boundary, and 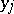 are fixed points in
are fixed points in 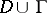 . This equation may also be written as
. This equation may also be written as
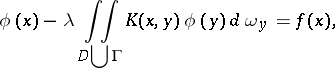 |
if the function 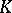 and the volume element
and the volume element 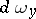 are correspondingly defined. In this case, moreover, the theory of Fredholm integral equations remains valid.
are correspondingly defined. In this case, moreover, the theory of Fredholm integral equations remains valid.
References
| [1] | A. Kneser, "Belastete Integralgleichungen" Rend. Circolo Mat. Palermo , 37 (1914) pp. 169–197 |
| [2] | L. Lichtenstein, "Bemerkungen über belastete Integralgleichungen" Studia Math. , 3 (1931) pp. 212–225 |
| [3] | N.M. Gunter, "Sur le problème des "Belastete Integralgleichungen" " Studia Math. , 4 (1933) pp. 8–14 |
| [4] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
Mixed integral equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mixed_integral_equation&oldid=18355