Abhyankar–Moh theorem
An affine algebraic variety 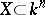 (with
(with 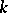 an algebraically closed field of characteristic zero) is said to have the Abhyankar–Moh property if every imbedding
an algebraically closed field of characteristic zero) is said to have the Abhyankar–Moh property if every imbedding 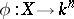 extends to an automorphism of
extends to an automorphism of 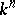 . The original Abhyankar–Moh theorem states that an imbedded affine line in
. The original Abhyankar–Moh theorem states that an imbedded affine line in 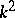 has the Abhyankar–Moh property, [a1].
has the Abhyankar–Moh property, [a1].
The algebraic version of this theorem (which works over any field) is as follows. Let 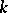 be a field of characteristic
be a field of characteristic 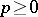 . Let
. Let 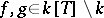 be such that
be such that 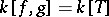 . Let
. Let 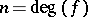 and
and 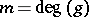 . If
. If 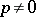 , suppose in addition that
, suppose in addition that 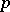 does not divide
does not divide 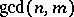 . Then
. Then 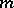 divides
divides  or
or  divides
divides 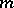 .
.
If 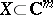 has
has 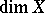 small in comparison with
small in comparison with  and has "nice" singularities, then
and has "nice" singularities, then 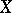 has the Abhyankar–Moh property [a2], [a4], [a5]. For every
has the Abhyankar–Moh property [a2], [a4], [a5]. For every  , the
, the  -cross
-cross 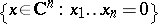 has the Abhyankar–Moh property, [a3]. The case of a hyperplane in
has the Abhyankar–Moh property, [a3]. The case of a hyperplane in 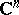 is still open (1998).
is still open (1998).
References
| [a1] | S.S. Abhyankar, T-t. Moh, "Embeddings of the line in the plane" J. Reine Angew. Math. , 276 (1975) pp. 148–166 |
| [a2] | Z. Jelonek, "A note about the extension of polynomial embeddings" Bull. Polon. Acad. Sci. Math. , 43 (1995) pp. 239–244 |
| [a3] | Z. Jelonek, "A hypersurface that has the Abhyankar–Moh property" Math. Ann. , 308 (1997) pp. 73–84 |
| [a4] | S. Kalliman, "Extensions of isomrphisms between affine algebraic subvarieties of 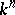 to automorphisms of to automorphisms of 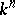 " Proc. Amer. Math. Soc. , 113 (1991) pp. 325–334 " Proc. Amer. Math. Soc. , 113 (1991) pp. 325–334 |
| [a5] | V. Srinivas, "On the embedding dimension of the affine variety" Math. Ann. , 289 (1991) pp. 125–132 |
Abhyankar–Moh theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abhyankar%E2%80%93Moh_theorem&oldid=17704