Telegraph equation

The partial differential equation

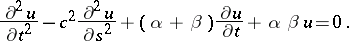(1)

This equation is satisfied by the intensity of the current in a conductor, considered as a function of time 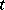and distance from any fixed point of the conductor. Here, is the speed of light, 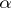is a capacity coefficient and 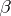is the induction coefficient.

By the transformation

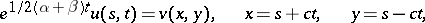equation (1) is reduced to the form

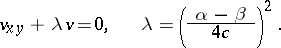(2)

This equation belongs to the class of hyperbolic equations of the second order (cf. Hyperbolic partial differential equation),

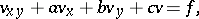in the theory of which an important part is played by the Riemann function 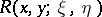. For equation (2) this function can be written in the explicit form

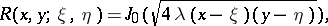where 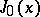is the Bessel function (cf. Bessel functions).

References

[1]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)

Comments

The special case 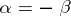is treated in [a1].

References

[a1]	F. John, "Partial differential equations" , Springer (1978)