Surface of screw motion
From Encyclopedia of Mathematics
helical surface
A surface described by a plane curve 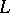 which, while rotating around an axis at a uniform rate, also advances along that axis at a uniform rate. If
which, while rotating around an axis at a uniform rate, also advances along that axis at a uniform rate. If 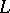 is located in the plane of the axis of rotation
is located in the plane of the axis of rotation  and is defined by the equation
and is defined by the equation 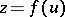 , the position vector of the surface of screw motion is
, the position vector of the surface of screw motion is
 |
and its line element is
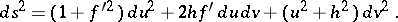 |
A surface of screw motion can be deformed into a rotation surface so that the generating helical lines are parallel (Boor's theorem). If 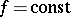 , one has a helicoid; if
, one has a helicoid; if  , one has a rotation surface, or surface of revolution.
, one has a rotation surface, or surface of revolution.
Comments
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a3] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 145 |
How to Cite This Entry:
Surface of screw motion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Surface_of_screw_motion&oldid=17025
Surface of screw motion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Surface_of_screw_motion&oldid=17025
This article was adapted from an original article by I.Kh. Sabitov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article