Mediant
From Encyclopedia of Mathematics
of two fractions 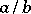 and
and 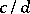 with positive denominators
with positive denominators
The fraction 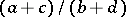 . The mediant of two fractions is positioned between them, i.e. if
. The mediant of two fractions is positioned between them, i.e. if 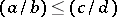 ,
, 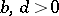 , then
, then
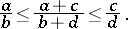 |
A finite sequence of fractions in which each intermediary term is the mediant of its two adjacent fractions is called a Farey series. The mediant of two adjacent convergent fractions of the continued-fraction expansion of a real number  is positioned between
is positioned between  and the convergent fraction of lower order (cf. also Continued fraction). Thus, if
and the convergent fraction of lower order (cf. also Continued fraction). Thus, if 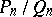 and
and 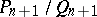 are convergent fractions of orders
are convergent fractions of orders  and
and 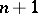 in the continued-fraction expansion of
in the continued-fraction expansion of 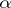 , then
, then
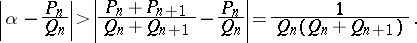 |
References
| [1] | A.Ya. Khinchin, "Continued fractions" , Univ. Chicago Press (1964) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
How to Cite This Entry:
Mediant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mediant&oldid=16953
Mediant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mediant&oldid=16953
This article was adapted from an original article by V.I. Nechaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article