Totally-irreducible set
A set 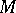 of linear operators (cf. Linear operator) on a locally convex topological vector space
of linear operators (cf. Linear operator) on a locally convex topological vector space  that is everywhere dense in the algebra
that is everywhere dense in the algebra 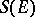 of all weakly-continuous linear operators on
of all weakly-continuous linear operators on  (cf. Weak topology); in this context
(cf. Weak topology); in this context 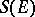 is considered with the weak operator topology. The concept of a totally-irreducible set, initially introduced for Banach spaces, also proved useful in the theory of group representations, mainly for semi-simple Lie groups. If
is considered with the weak operator topology. The concept of a totally-irreducible set, initially introduced for Banach spaces, also proved useful in the theory of group representations, mainly for semi-simple Lie groups. If 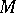 is a totally-irreducible set, it is also topologically irreducible, i.e. any closed subspace of
is a totally-irreducible set, it is also topologically irreducible, i.e. any closed subspace of 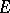 which is invariant with respect to
which is invariant with respect to  coincides with zero or with the entire space
coincides with zero or with the entire space 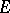 . If
. If 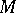 is a totally-irreducible set, its commutator subset in
is a totally-irreducible set, its commutator subset in 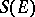 consists of the operators that are multiples of the identity. The property of total irreducibility is equivalent to that of topological irreducibility in the following cases: 1)
consists of the operators that are multiples of the identity. The property of total irreducibility is equivalent to that of topological irreducibility in the following cases: 1) 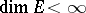 ; or 2)
; or 2) 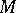 is a semi-group of unitary operators on a Hilbert space.
is a semi-group of unitary operators on a Hilbert space.
References
| [1] | D.P. Zhelobenko, "Harmonic analysis of functions on semi-simple complex Lie groups" , Moscow (1974) (In Russian) |
Comments
A set 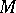 of operators on a vector space
of operators on a vector space  is algebraically irreducible if there are no proper subspaces of
is algebraically irreducible if there are no proper subspaces of 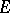 (i.e. except
(i.e. except 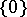 and
and 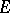 ) that are invariant under all
) that are invariant under all 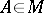 . Cf. also Irreducible representation. A totally-irreducible set is also called completely irreducible.
. Cf. also Irreducible representation. A totally-irreducible set is also called completely irreducible.
The link between topological irreducibility and algebraic irreducibility and the statement that the commutator subset of  consists of multiples of the identity is provided by the Schur lemma. For a finite-dimensional space
consists of multiples of the identity is provided by the Schur lemma. For a finite-dimensional space 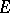 over a field
over a field 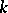 , the algebraic (or topological) irreducibility of a set of operators implies that the commutator subset in
, the algebraic (or topological) irreducibility of a set of operators implies that the commutator subset in 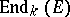 is a division algebra over
is a division algebra over 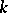 in general, and equal to
in general, and equal to 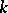 if
if 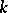 is algebraically closed. If
is algebraically closed. If 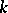 is not algebraically closed, this need not be the case. E.g., if
is not algebraically closed, this need not be the case. E.g., if  , the commutant of an irreducible representation of a group can be
, the commutant of an irreducible representation of a group can be 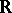 ,
, 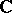 or the four-dimensional algebra of quaternions over
or the four-dimensional algebra of quaternions over 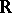 . Thus, the statement above about the equivalence for finite-dimensional
. Thus, the statement above about the equivalence for finite-dimensional 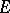 between algebraic irreducibility (or, what is the same in this case, topological irreducibility) holds for algebraically closed ground fields but it does not hold for a non-algebraically closed ground field. For instance, if
between algebraic irreducibility (or, what is the same in this case, topological irreducibility) holds for algebraically closed ground fields but it does not hold for a non-algebraically closed ground field. For instance, if 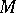 is the collection of operators
is the collection of operators
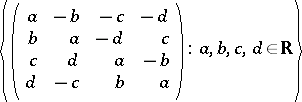 |
(the left regular representation of the quaternion algebra on itself), then 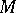 is algebraically irreducible, but its commutant algebra is the four-dimensional algebra of all matrices of the form
is algebraically irreducible, but its commutant algebra is the four-dimensional algebra of all matrices of the form
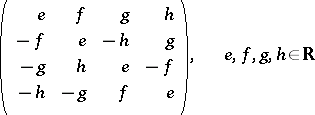 |
(another copy inside 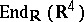 of the quaternion algebra, corresponding to the right regular representation).
of the quaternion algebra, corresponding to the right regular representation).
References
| [a1] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979) pp. 47 |
| [a2] | J. Dixmier, "Les 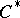 -algèbres et leur représentations" , Gauthier-Villars (1964) pp. §2.3 -algèbres et leur représentations" , Gauthier-Villars (1964) pp. §2.3 |
Totally-irreducible set. D.P. Zhelobenko (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Totally-irreducible_set&oldid=16764