Bertini theorems
Two theorems concerning the properties of linear systems (cf. Linear system) on algebraic varieties, due to E. Bertini [1].
Let  be an algebraic variety over an algebraically closed field
be an algebraic variety over an algebraically closed field  of characteristic 0, let
of characteristic 0, let  be a linear system without fixed components on
be a linear system without fixed components on  and let
and let  be the image of the variety
be the image of the variety  under the mapping given by
under the mapping given by  . The following two theorems are known as the first and the second Bertini theorem, respectively.
. The following two theorems are known as the first and the second Bertini theorem, respectively.
1) If  , then almost all the divisors of the linear system
, then almost all the divisors of the linear system  (i.e. all except a closed subset in the parameter space
(i.e. all except a closed subset in the parameter space 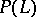 not equal to
not equal to 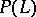 ) are irreducible reduced algebraic varieties.
) are irreducible reduced algebraic varieties.
2) Almost all divisors of 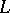 have no singular points outside the basis points of the linear system
have no singular points outside the basis points of the linear system 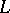 and the singular points of the variety
and the singular points of the variety 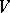 .
.
Both Bertini theorems are invalid if the characteristic of the field is non-zero.
Conditions under which Bertini's theorems are valid for the case of a finite characteristic of the field have been studied [3], [6]. If 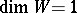 , Bertini's theorem is replaced by the following theorem: Almost all fibres of the mapping
, Bertini's theorem is replaced by the following theorem: Almost all fibres of the mapping  are irreducible and reduced if the function field
are irreducible and reduced if the function field 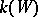 is algebraically closed in the field
is algebraically closed in the field 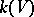 under the imbedding
under the imbedding 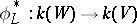 . If the characteristic of
. If the characteristic of 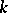 is finite, the corresponding theorem is true if the extension
is finite, the corresponding theorem is true if the extension 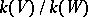 is separable [3], [6]. The Bertini theorems apply to linear systems of hyperplane sections, without restrictions on the characteristic of the field [5].
is separable [3], [6]. The Bertini theorems apply to linear systems of hyperplane sections, without restrictions on the characteristic of the field [5].
References
| [1] | E. Bertini, "Introduction to the projective geometry of hyperspaces" , Messina (1923) (In Italian) |
| [2] | "Algebraic surfaces" Trudy Mat. Inst. Steklov. , 75 (1965) (In Russian) |
| [3] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [4] | Y. Akizuki, "Theorems of Bertini on linear systems" J. Math. Soc. Japan , 3 : 1 (1951) pp. 170–180 |
| [5] | Y. Nakai, "Note on the intersection of an algebraic variety with the generic hyperplane" Mem. Coll. Sci. Univ. Kyoto Ser. A Math. , 26 : 2 (1950) pp. 185–187 |
| [6] | O. Zariski, "The theorem of Bertini on the variable singular points of a linear system of varieties" Trans. Amer. Math. Soc. , 56 (1944) pp. 130–140 |
| [7] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Bertini theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bertini_theorems&oldid=16310