Hypercontractive semi-group
A semi-group  of Hermitian operators (cf. also Semi-group of operators) on a Hilbert space
of Hermitian operators (cf. also Semi-group of operators) on a Hilbert space  such that:
such that:
1) 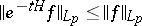 for all
for all  ,
,  and
and  ;
;
2) there exist  and
and  such that
such that  for all
for all  . Semi-groups having properties similar to 1) and 2) were first introduced by E. Nelson [a9] to prove that the Hamiltonian operators arising in some models of quantum field theory are bounded below. In the important case that
. Semi-groups having properties similar to 1) and 2) were first introduced by E. Nelson [a9] to prove that the Hamiltonian operators arising in some models of quantum field theory are bounded below. In the important case that  , condition 2) can be replaced by the following more natural condition, to which 2) is equivalent in the presence of 1):
, condition 2) can be replaced by the following more natural condition, to which 2) is equivalent in the presence of 1):
3) for every  there exists a
there exists a  , depending on
, depending on 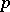 and
and  , such that
, such that  (restricted or extended to
(restricted or extended to  ) is a bounded operator from
) is a bounded operator from  to
to 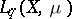 . Interpolation theorems are used in the proof. Below, all
. Interpolation theorems are used in the proof. Below, all  spaces are taken to be real for simplicity and it is assumed that
spaces are taken to be real for simplicity and it is assumed that  , this being the case of principal interest.
, this being the case of principal interest.
The prototypical example of a hypercontractive semi-group is given by choosing  and
and
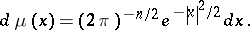 |
Denote by  the adjoint of differentiation computed in
the adjoint of differentiation computed in  . Let
. Let
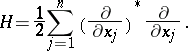 |
(This should be interpreted as a closed version of the Ornstein–Uhlenbeck operator with  as a core.) Then
as a core.) Then  is a hypercontractive semi-group. In fact,
is a hypercontractive semi-group. In fact, 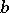 can be taken equal to one in condition 2). Furthermore, for this semi-group the smallest time
can be taken equal to one in condition 2). Furthermore, for this semi-group the smallest time 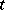 for boundedness in condition 3) is known. One has Nelson's family of hypercontractive inequalities: for
for boundedness in condition 3) is known. One has Nelson's family of hypercontractive inequalities: for 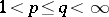 ,
,
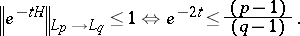 | (a1) |
Moreover,  if
if  . In (a1) one should regard the operators
. In (a1) one should regard the operators  as restricted or extended to
as restricted or extended to  .
.
If in (a1) one chooses  and
and  , then (a1) yields
, then (a1) yields
 | (a2) |
This inequality becomes an equality for  . Therefore it can be differentiated at
. Therefore it can be differentiated at  for
for  smooth enough. One gets the following logarithmic Sobolev inequality [a7]:
smooth enough. One gets the following logarithmic Sobolev inequality [a7]:
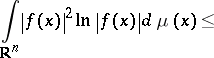 | (a3) |
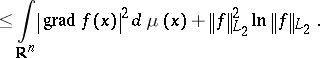 |
Nelson's family of hypercontractive inequalities (a1) can be recovered easily from the single logarithmic Sobolev inequality (a3) [a7]. More generally, L. Gross [a7] established an equivalence between hypercontractivity conditions such as 1) and 2), on the one hand, and, on the other hand, coercivity inequalities for 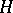 of the form
of the form
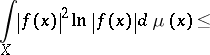 | (a4) |
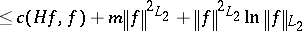 |
(which reduces to (a3) in the previous example if one takes  and
and  ). These coercivity inequalities have come to be known in general as logarithmic Sobolev inequalities. Because of this equivalence the theory of hypercontractive semi-groups has, to a great extent, been developed in conjunction with the theory of logarithmic Sobolev inequalities. The equivalence of (a4) with 1) and 2) is valid only for a class of operators
). These coercivity inequalities have come to be known in general as logarithmic Sobolev inequalities. Because of this equivalence the theory of hypercontractive semi-groups has, to a great extent, been developed in conjunction with the theory of logarithmic Sobolev inequalities. The equivalence of (a4) with 1) and 2) is valid only for a class of operators  which includes the important category of Dirichlet-form operators. See the survey [a8] for further generality and for references to the early history of these two topics.
which includes the important category of Dirichlet-form operators. See the survey [a8] for further generality and for references to the early history of these two topics.
By way of application, if one can establish inequalities of the form (a4) for an elliptic partial differential operator 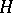 on a Riemannian manifold, then one half of the equivalence theorem shows that the semi-group
on a Riemannian manifold, then one half of the equivalence theorem shows that the semi-group 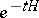 has boundedness properties similar to 3), with a specifically given function
has boundedness properties similar to 3), with a specifically given function  . Since
. Since 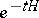 is an integral operator, with kernel
is an integral operator, with kernel  say, these norm bounds on
say, these norm bounds on  can be converted into direct estimates on the size of the so-called "heat kernel"
can be converted into direct estimates on the size of the so-called "heat kernel"  . See [a4] for a self-contained exposition of this method of obtaining pointwise heat kernel bounds for elliptic partial differential operators.
. See [a4] for a self-contained exposition of this method of obtaining pointwise heat kernel bounds for elliptic partial differential operators.
There are three basic consequences of the logarithmic Sobolev inequality (a4) which do not require  to be a Dirichlet-form operator but merely self-adjoint (cf. Self-adjoint operator).
to be a Dirichlet-form operator but merely self-adjoint (cf. Self-adjoint operator).
i) The Federbush–Faris semi-boundedness theorem asserts that (a4) is equivalent to the condition that the (generally unbounded) operator  is in fact bounded below for all real-valued measurable functions
is in fact bounded below for all real-valued measurable functions  on
on  satisfying
satisfying 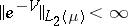 .
.
ii) The Segal–Faris additivity theorem asserts that if 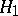 and
and 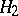 both satisfy (a4), then so does the independent sum
both satisfy (a4), then so does the independent sum 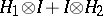 .
.
iii) The Rothaus–Simon spectral gap theorem asserts that if (a4) holds with  and if
and if  , then
, then  has no spectrum (cf. Spectrum of an operator) in the interval
has no spectrum (cf. Spectrum of an operator) in the interval  . For precise statements of these theorems and proofs see the survey [a8].
. For precise statements of these theorems and proofs see the survey [a8].
A very simple example of another semi-group satisfying Nelson's hypercontractivity inequalities (a1) is as follows. Denote by 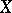 the two-point set
the two-point set  . Define
. Define  . Let
. Let  be the projection onto the orthogonal complement of the constant functions in
be the projection onto the orthogonal complement of the constant functions in  . Then (a1) holds. Moreover, (a4) holds with
. Then (a1) holds. Moreover, (a4) holds with 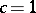 and
and  . Since
. Since  is two-dimensional, the proof of (a4) reduces in this example to a few lines of elementary calculus (see, e.g., [a8], Example 2.6). The resulting inequality is known as the two-point logarithmic Sobolev inequality. Now, by the Segal–Faris additivity theorem there follows by induction a logarithmic Sobolev inequality on the product space
is two-dimensional, the proof of (a4) reduces in this example to a few lines of elementary calculus (see, e.g., [a8], Example 2.6). The resulting inequality is known as the two-point logarithmic Sobolev inequality. Now, by the Segal–Faris additivity theorem there follows by induction a logarithmic Sobolev inequality on the product space  for the product measure. An application of the central limit theorem then allows one to take the limit as
for the product measure. An application of the central limit theorem then allows one to take the limit as  and arrive at the inequality (a3) (first for
and arrive at the inequality (a3) (first for 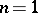 , then, by additivity, for general
, then, by additivity, for general  ). This method of deriving the differential inequalities (a1) from discrete inequalities via the central limit theorem [a3], [a7] has also been used [a2] to derive the sharp Hausdorff–Young inequality (cf. Hausdorff–Young inequalities) for the Fourier transform on
). This method of deriving the differential inequalities (a1) from discrete inequalities via the central limit theorem [a3], [a7] has also been used [a2] to derive the sharp Hausdorff–Young inequality (cf. Hausdorff–Young inequalities) for the Fourier transform on  .
.
The notions of hypercontractivity and logarithmic Sobolev inequalities can also be formulated in the context of non-commutative integration theory, specifically over Clifford algebras (cf. Clifford algebra). See [a8], Sect. 6(v), for a survey.
Applications of both concepts to statistical mechanics are rapidly increasing at the present time (1996). For a survey of work through 1992, see [a10]. For applications to the theory of large deviations, see [a5]. For recent applications to statistics, see the survey [a6].
Unlike the classical Sobolev inequalities, logarithmic Sobolev inequalities tend to be dimension independent and valid in many infinite-dimensional settings. For example, the inequality (a3) is meaningful and correct when 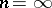 . One need only interpret the first integrand on the right as
. One need only interpret the first integrand on the right as
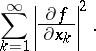 |
The dimension independence accounts, in part, for their usefulness in statistical mechanics (cf. also Statistical mechanics, mathematical problems in), statistics, and large deviations, and for their origin in constructive quantum field theory.
The survey [a8] discusses the topics up through 1992. [a1] also surveys related topics and describes various methods for proving logarithmic Sobolev inequalities for specific operators  .
.
References
| [a1] | D. Bakry, "L'hypercontractivité et son utilisation en théorie des semi-groups" P. Bernard (ed.) , Lectures on Probability Theory , Lecture Notes in Mathematics , 1581 , Springer (1994) pp. 1–114 |
| [a2] | W. Beckner, "Inequalities in Fourier analysis" Ann. of Math. , 102 (1975) pp. 159–182 |
| [a3] | A. Bonami, "Études des coefficients de Fourier des fonctions de 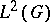 " Ann. Inst. Fourier , 20 : 2 (1970) pp. 335–402 " Ann. Inst. Fourier , 20 : 2 (1970) pp. 335–402 |
| [a4] | E.B. Davies, "Heat kernels and spectral theory" , Cambridge Univ. Press (1989) |
| [a5] | J. D. Deuschel, D. W. Stroock, "Large deviations" , Pure Appl. Math. , 137 , Acad. Press (1989) |
| [a6] | P. Diaconis, L. Saloff-Coste, "Logarithmic Sobolev inequalities for finite Markov chains" Ann. Appl. Probab. (1996) |
| [a7] | L. Gross, "Logarithmic Sobolev inequalities" Amer. J. of Math. , 97 (1975) pp. 1061–1083 |
| [a8] | L. Gross, "Logarithmic Sobolev inequalities and contractivity properties of semigroups" G. Dell'Antonio (ed.) U. Mosco (ed.) , Dirichlet Forms , Lecture Notes in Mathematics , 1563 , Springer (1993) pp. 54–88 |
| [a9] | E. Nelson, "A quartic interaction in two dimensions" R. Goodman (ed.) I.E. Segal (ed.) , Mathematical Theory of Elementary Particles , MIT (1966) pp. 69–73 |
| [a10] | D. Stroock, "Logarithmic Sobolev inequalities for Gibbs states" G. Dell'Antonio (ed.) U. Mosco (ed.) , Dirichlet Forms , Lecture Notes in Mathematics , 1563 , Springer (1993) pp. 194–228 |
Hypercontractive semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hypercontractive_semi-group&oldid=15980