Lamé constants
From Encyclopedia of Mathematics
Quantities that connect the components of an elastic stress at some point of a linearly-elastic (or solid deformable) isotropic body with the components of the deformation at this point:
 |
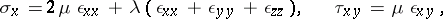where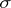 
and 
are the normal and tangential constituents of the stress, 
are the components of the deformation and the coefficients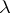 
and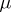 
are the Lamé constants. The Lamé constants depend on the material and its temperature. The Lamé constants are connected with the elasticity modulus 
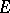and Poisson's ratio 
by
 |
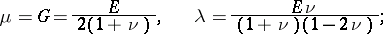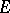is also called Young's modulus and 
is the modulus of shear.
The Lamé constants are named after G. Lamé.
Comments
References
| [a1] | E.M. Lifshitz, "Theory of elasticity" , Pergamon (1959) (Translated from Russian) |
| [a2] | I.S. [I.S. Sokolnikov] Sokolnikoff, "Mathematical theory of elasticity" , McGraw-Hill (1956) (Translated from Russian) |
| [a3] | S.C. Hunter, "Mechanics of continuous media" , Wiley (1976) |
How to Cite This Entry:
Lamé constants. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lam%C3%A9_constants&oldid=15506
Lamé constants. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lam%C3%A9_constants&oldid=15506
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article