Domain of influence
of a point 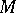 (of a set
(of a set 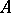 of points
of points 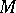 )
)
The set 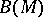 (respectively,
(respectively, 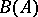 ) of all points at which the solution of a differential equation or of a set of differential equations changes as a result of a perturbation of it at the point
) of all points at which the solution of a differential equation or of a set of differential equations changes as a result of a perturbation of it at the point 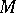 (or at the set
(or at the set 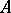 ). In the simplest cases of linear partial differential equations the domain of influence is independent of the solution; for most non-linear problems the domain of influence depends both on the solution itself and on the nature of the perturbations. In such a case infinitely small perturbations are considered. For hyperbolic equations, the domain of influence of the point
). In the simplest cases of linear partial differential equations the domain of influence is independent of the solution; for most non-linear problems the domain of influence depends both on the solution itself and on the nature of the perturbations. In such a case infinitely small perturbations are considered. For hyperbolic equations, the domain of influence of the point 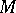 is often the union of the characteristic conoid (cf. Characteristic manifold) passing through the point
is often the union of the characteristic conoid (cf. Characteristic manifold) passing through the point 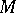 and its interior; for parabolic and elliptic equations, the domain of influence of the point
and its interior; for parabolic and elliptic equations, the domain of influence of the point 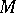 is usually the domain of definition of the solution.
is usually the domain of definition of the solution.
Comments
This notion is usually met in the context of initial value problems (also called Cauchy problems, cf. Cauchy problem) for first-order, or general hyperbolic, partial differential equations (cf. Differential equation, partial, of the first order; Hyperbolic partial differential equation). For a more precise discussion of the latter case see [a1], Chapt. 6 Par. 7.
A related notion is that of the domain of dependence (cf. Cauchy problem).
References
| [a1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
Domain of influence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Domain_of_influence&oldid=15452