Blackwell renewal theorem
Consider a piece of equipment that has a finite but random life-time. Suppose one starts with a new one and, after that fails, replaces it with a second new one and, after that one fails, replaces it with a third new one and so on indefinitely. Such a process is called a renewal process (cf. also Renewal theory) and objects of interest are the behaviour for large (time) 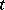 :
:
i) of the average number of units replaced in the interval 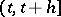 , where
, where 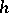 is fixed;
is fixed;
ii) of the probability of renewal at time 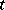 ;
;
iii) of the age, the remaining life and the total life of the (current) unit in operation at time 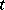 . The mathematical theory of such processes is called renewal theory and Blackwell's renewal theorem plays a central role in it. See [a2], [a4], [a5].
. The mathematical theory of such processes is called renewal theory and Blackwell's renewal theorem plays a central role in it. See [a2], [a4], [a5].
Mathematical framework.
Let  be a sequence of independent and identically distributed random variables that are non-negative (cf. also Random variable). The value of
be a sequence of independent and identically distributed random variables that are non-negative (cf. also Random variable). The value of 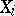 is to be thought of as the life-length of the
is to be thought of as the life-length of the 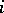 th unit. Let, for
th unit. Let, for 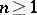 ,
,
 | (a1) |
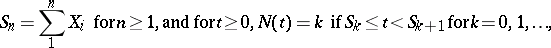 |
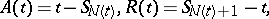 |
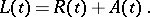 |
Thus, 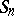 is the time of the
is the time of the  th renewal,
th renewal, 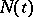 is the number of units used up to time
is the number of units used up to time 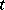 excluding the one in operation,
excluding the one in operation, 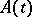 is the age of the unit in place at time
is the age of the unit in place at time 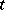 with
with 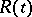 being its remaining life-time and
being its remaining life-time and 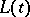 its total life-time. Let
its total life-time. Let
 | (a2) |
where 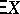 denotes the expected value, or mathematical expectation, of the random variable
denotes the expected value, or mathematical expectation, of the random variable  .
.
Blackwell's renewal theorem says that for fixed 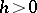 ,
,  converges as
converges as 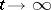 to
to 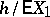 . A precise statement is given below. This was proved by D. Blackwell; see [a2]. This result has several variants and consequences and applications in applied probability theory; see [a1].
. A precise statement is given below. This was proved by D. Blackwell; see [a2]. This result has several variants and consequences and applications in applied probability theory; see [a1].
Let 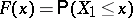 be the distribution function of the random variable
be the distribution function of the random variable 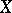 (cf. also Distribution function); it is assumed that
(cf. also Distribution function); it is assumed that  . The function
. The function  is said to be arithmetic if there exist
is said to be arithmetic if there exist 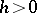 and
and 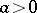 such that
such that
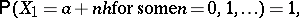 |
i.e. 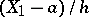 is a non-negative integer-valued random variable. The largest
is a non-negative integer-valued random variable. The largest 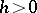 for which this holds is called the span; see [a5].
for which this holds is called the span; see [a5]. 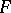 is said to be non-arithmetic if it is not arithmetic.
is said to be non-arithmetic if it is not arithmetic.
Blackwell's renewal theorem.
Arithmetic case.
Let  be arithmetic with
be arithmetic with 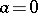 and span
and span 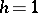 . Let, for
. Let, for 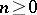 ,
,
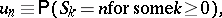 | (a3) |
i.e. the probability that there is a renewal at time  . Then
. Then
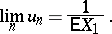 | (a4) |
Non-arithmetic case.
Let  be non-arithmetic. Then for any
be non-arithmetic. Then for any 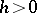 ,
,
 | (a5) |
The arithmetic case was proved by P. Erdös, W. Feller and H. Pollard; see [a4]. The non-arithmetic case was proved by Blackwell; see [a5]. More recently, proofs of these using the coupling method have become available (see [a3]).
Key renewal theorem.
There is an equivalent of this result, known as the key renewal theorem. It is as follows. Since 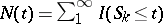 , its expected value
, its expected value 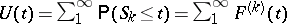 , where
, where 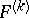 is the
is the 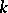 fold convolution of
fold convolution of 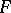 , defined by
, defined by
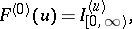 |
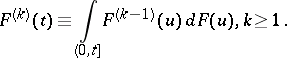 |
A discrete renewal equation, with probability distribution 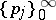 and forcing sequence
and forcing sequence  is an equation for a sequence
is an equation for a sequence  that satisfies
that satisfies
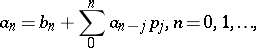 | (a6) |
where it is assumed that  ,
, 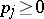 and
and 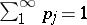 .
.
A renewal equation with distribution  and forcing function
and forcing function  is an equation for a function
is an equation for a function 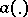 where both
where both  and
and 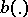 are functions
are functions 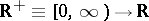 that are Borel measurable and bounded on finite intervals and satisfy
that are Borel measurable and bounded on finite intervals and satisfy
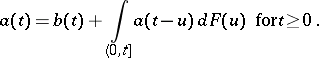 | (a7) |
It can be shown that (a6) and (a7) have unique solutions given by, respectively,
 | (a8) |
and
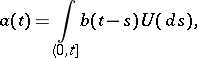 | (a9) |
where 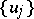 is as in (a3) and
is as in (a3) and 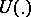 is as in (a2).
is as in (a2).
A function 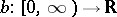 is called directly Riemann integrable if for every
is called directly Riemann integrable if for every 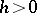 ,
,
 |
and as 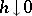 and
and 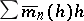 and
and 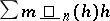 approach the same limit, where
approach the same limit, where 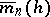 and
and 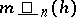 are, respectively, the supremum and infimum of
are, respectively, the supremum and infimum of 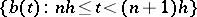 . This common limit is usually denoted by
. This common limit is usually denoted by 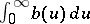 ; see [a5]. A very useful equivalent of the Blackwell renewal theorem is the key renewal theorem.
; see [a5]. A very useful equivalent of the Blackwell renewal theorem is the key renewal theorem.
Arithmetic case.
Let 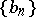 satisfy
satisfy 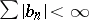 and
and 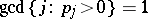 . Then the unique solution
. Then the unique solution 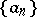 to (a6) is given by (a8) and
to (a6) is given by (a8) and
 |
Non-arithmetic case.
Let 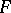 be non-arithmetic and let
be non-arithmetic and let  be directly Riemann integrable. Then the unique solution
be directly Riemann integrable. Then the unique solution 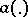 to (a7) is given by (a9) and
to (a7) is given by (a9) and
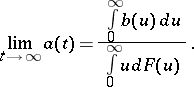 |
Application.
A random or stochastic process 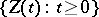 in discrete or continuous time is called regenerative if there exist a sequence of random times
in discrete or continuous time is called regenerative if there exist a sequence of random times 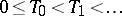 such that
such that 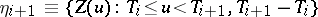 ,
, 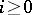 , are stochastically independent, identically distributed and independent of
, are stochastically independent, identically distributed and independent of 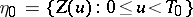 . Let
. Let  be a measurable function on the state space of
be a measurable function on the state space of 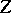 and
and 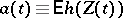 . Then
. Then 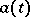 satisfies the renewal equation (a7) with
satisfies the renewal equation (a7) with 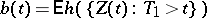 and
and 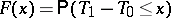 . So, if the distribution of
. So, if the distribution of 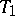 is non-arithmetic, then from the key renewal theorem one can conclude that
is non-arithmetic, then from the key renewal theorem one can conclude that
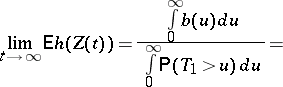 |
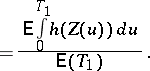 |
This, in turn, can be used to prove the convergence to an equilibrium distribution for many regenerative processes, including positive recurrent irreducible Markov chains; see [a1].
References
| [a1] | S. Asmussen, "Applied probability and queues" , Wiley (1987) |
| [a2] | D. Blackwell, "A renewal theorem" Duke Math. J. , 15 (1948) pp. 145–150 |
| [a3] | T. Lindvall, "Lectures on the coupling method" , II , Wiley (1992) (Edition: Second) |
| [a4] | W. Feller, "An introduction to probability theory and its applications" , 1 , Wiley (1968) (Edition: Third) |
| [a5] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1970) (Edition: Second) |
Blackwell renewal theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blackwell_renewal_theorem&oldid=14923