Variety of semi-groups
A class of semi-groups (cf. Semi-group) defined by a system of identities, or laws (see Algebraic systems, variety of). Every variety of semi-groups is either periodic, i.e. it consists of periodic semi-groups, or overcommutative, i.e. it contains the variety of all commutative semi-groups. Various properties of varieties of semi-groups are classified by singling out certain types of identities. An identity  is said to be normal (also homotypical, regular or uniform) if the sets of variables figuring in the words
is said to be normal (also homotypical, regular or uniform) if the sets of variables figuring in the words  and
and  are the same, and anomalous (or heterotypical) otherwise. An identity
are the same, and anomalous (or heterotypical) otherwise. An identity  is said to be balanced if each variable appears in
is said to be balanced if each variable appears in  just as many times as it does in
just as many times as it does in  . A special case of a balanced identity is a permutation identity — if
. A special case of a balanced identity is a permutation identity — if  and
and  is obtained from
is obtained from  by permuting the variables. A variety of semi-groups is overcommutative if and only if all its identities are balanced. A basis of identities for a variety of semi-groups
by permuting the variables. A variety of semi-groups is overcommutative if and only if all its identities are balanced. A basis of identities for a variety of semi-groups 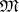 is said to be irreducible if any of its proper subsets defines a variety distinct from
is said to be irreducible if any of its proper subsets defines a variety distinct from 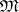 . Every overcommutative variety of semi-groups has an irreducible basis of identities. There exist varieties of semi-groups which do not have irreducible bases of identities. Examples of varieties of semi-groups with finite bases are: any variety of commutative semi-groups; any periodic variety of semi-groups with a permutation identity; any variety of semi-groups defined by permutation identities. Any semi-group with less than six elements has a finite basis of identities, but there exists a
. Every overcommutative variety of semi-groups has an irreducible basis of identities. There exist varieties of semi-groups which do not have irreducible bases of identities. Examples of varieties of semi-groups with finite bases are: any variety of commutative semi-groups; any periodic variety of semi-groups with a permutation identity; any variety of semi-groups defined by permutation identities. Any semi-group with less than six elements has a finite basis of identities, but there exists a 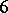 -element semi-group that has no finite basis of identities.
-element semi-group that has no finite basis of identities.
The following conditions for a variety of semi-groups 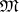 are equivalent:
are equivalent: 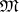 is defined by normal identities; all identities of
is defined by normal identities; all identities of 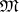 are normal;
are normal; 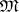 contains a two-element semi-lattice. Among the identities of a variety of semi-groups
contains a two-element semi-lattice. Among the identities of a variety of semi-groups 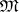 there is an anomalous one if and only if
there is an anomalous one if and only if 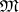 is periodic and consists of Archimedean semi-groups (cf. Archimedean semi-group).
is periodic and consists of Archimedean semi-groups (cf. Archimedean semi-group).
The minimal varieties of semi-groups are exhausted by the varieties of all: 1) semi-lattices; 2) semi-groups of left zeros; 3) semi-groups of right zeros (see Idempotents, semi-group of); 4) semi-groups with zero multiplication; 5) Abelian groups of exponent 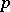 for any prime number
for any prime number 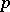 . In the lattice of all varieties of semi-groups, every non-unit element has an element that covers it; a unit element cannot be equal to the union of finitely many non-unit elements. The lattice of all varieties of semi-groups does not satisfy any non-trivial lattice identity and has the cardinality of the continuum. The sublattice of all varieties of nil-semi-groups with the identity
. In the lattice of all varieties of semi-groups, every non-unit element has an element that covers it; a unit element cannot be equal to the union of finitely many non-unit elements. The lattice of all varieties of semi-groups does not satisfy any non-trivial lattice identity and has the cardinality of the continuum. The sublattice of all varieties of nil-semi-groups with the identity 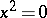 is also of the cardinality of the continuum, as is the sublattice of all overcommutative varieties. For some varieties of semi-groups
is also of the cardinality of the continuum, as is the sublattice of all overcommutative varieties. For some varieties of semi-groups 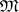 , explicit descriptions have been discovered for the lattice
, explicit descriptions have been discovered for the lattice 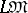 of subvarieties of it; there are also descriptions of varieties of semi-groups
of subvarieties of it; there are also descriptions of varieties of semi-groups 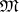 with certain restrictions on
with certain restrictions on 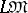 .
.
A variety of semi-groups is said to be small if 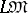 is finite. A variety of semi-groups
is finite. A variety of semi-groups  is called a variety of finite index if the degrees of nilpotency of the nilpotent semi-groups in
is called a variety of finite index if the degrees of nilpotency of the nilpotent semi-groups in 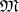 are uniformly bounded (equivalent conditions are: every nil-semi-group in
are uniformly bounded (equivalent conditions are: every nil-semi-group in 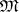 is nilpotent; or:
is nilpotent; or: 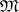 does not contain the variety of all commutative nil-semi-groups with the identity
does not contain the variety of all commutative nil-semi-groups with the identity  ). Every small variety of semi-groups is of finite index.
). Every small variety of semi-groups is of finite index.
If 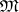 is a periodic variety of semi-groups, the following conditions are equivalent [4]:
is a periodic variety of semi-groups, the following conditions are equivalent [4]: 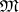 consists of bands of Archimedean semi-groups; in any semi-group in
consists of bands of Archimedean semi-groups; in any semi-group in  , every torsion class is a sub-semi-group;
, every torsion class is a sub-semi-group; 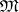 does not contain the Brandt semi-group
does not contain the Brandt semi-group 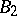 (see Periodic semi-group). These conditions are satisfied by varieties of semi-groups
(see Periodic semi-group). These conditions are satisfied by varieties of semi-groups  with a modular lattice
with a modular lattice 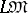 and varieties of semi-groups of finite index (in particular, small varieties). A small variety of semi-groups is locally finite (i.e. consists of locally finite semi-groups) if and only if the variety of all groups in
and varieties of semi-groups of finite index (in particular, small varieties). A small variety of semi-groups is locally finite (i.e. consists of locally finite semi-groups) if and only if the variety of all groups in 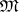 is locally finite; the small locally finite varieties of groups are precisely the Cross varieties (see Variety of groups). For other locally finite varieties of semi-groups, see Locally finite semi-group. There is a description of the varieties of semi-groups whose elements are residually-finite semi-groups [3].
is locally finite; the small locally finite varieties of groups are precisely the Cross varieties (see Variety of groups). For other locally finite varieties of semi-groups, see Locally finite semi-group. There is a description of the varieties of semi-groups whose elements are residually-finite semi-groups [3].
The set of all varieties of semi-groups forms a partial groupoid  relative to the Mal'tsev product. The idempotents of
relative to the Mal'tsev product. The idempotents of 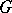 are known; there are just nine of them. The set of all varieties of semi-groups defined by systems of identities of the type
are known; there are just nine of them. The set of all varieties of semi-groups defined by systems of identities of the type 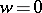 is a maximal groupoid in
is a maximal groupoid in 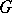 .
.
Studies have also been conducted on varieties of semi-groups with additional signature operations: varieties of monoids (with an identity, cf. Monoid); varieties of semi-groups with a zero; varieties of inverse semi-groups; etc.
References
| [1] | T. Evans, "The lattice of semigroup varieties" Semigroup Forum , 2 : 1 (1971) pp. 1–43 |
| [2] | A.Ya Aizenshtat, B.K. Boguta, , Semi-group varieties and semi-groups of endomorphisms , Leningrad (1979) pp. 3–46 (In Russian) |
| [3] | E.A. Golubov, M.V. Sapir, "Varieties of finitely approximable semigroups" Soviet Math. Dokl. , 20 : 4 (1979) pp. 828–832 Dokl. Akad. Nauk SSSR , 247 : 5 (1979) pp. 1037–1041 |
| [4] | M.V. Sapir, E.V. Sukhanov, "On manifolds of periodic semigroups" Soviet Math. Izv. Vyz. , 25 : 4 (1981) pp. 53–63 Izv. Vuzov. Mat. , 25 : 4 (1981) pp. 48–55 |
| [5] | L.N. Shevrin, M.V. Volkov, "Identities of semigroups" Soviet Math. Izv. Vyz. , 29 : 11 (1985) pp. 1–64 Izv. Vuzov. Mat. , 29 : 11 (1985) pp. 3–47 |
| [6] | L.N. Shevrin, E.V. Sukhanov, "Structural aspects of theory of semigroup varieties" Soviet Math. Izv. Vyz. , 33 : 6 (1989) pp. 1–34 Izv. Vuzov. Mat. , 33 : 6 (1989) pp. 3–39 |
Comments
References
| [a1] | E.S. [E.S. Lyapin] Ljapin, "Semigroups" , Amer. Math. Soc. (1978) pp. Chapt. XII (Translated from Russian) |
| [a2] | N.R. Reilly, "On the lattice of varieties of completely regular semigroups" S.M. Goberstein (ed.) P.M. Higgins (ed.) , Semigroups and Their Applications , Reidel (1987) pp. 153–167 |
Variety of semi-groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variety_of_semi-groups&oldid=14814