Random and pseudo-random numbers
Numbers 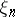 (in particular, binary digits
(in particular, binary digits 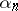 ) whose sequential appearance satisfies some kind of statistical regularity (see Probability theory). One distinguishes random numbers, being generated by a stochastic apparatus, and pseudo-random numbers, being constructed using arithmetical algorithms. It is usually assumed (for better or worse reason) that the sequence obtained (or constructed) has frequency properties that are "typical" for a sequence of independent realizations of some random variable
) whose sequential appearance satisfies some kind of statistical regularity (see Probability theory). One distinguishes random numbers, being generated by a stochastic apparatus, and pseudo-random numbers, being constructed using arithmetical algorithms. It is usually assumed (for better or worse reason) that the sequence obtained (or constructed) has frequency properties that are "typical" for a sequence of independent realizations of some random variable 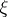 with distribution function
with distribution function 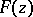 ; then one speaks of (independent) random numbers distributed according to the law
; then one speaks of (independent) random numbers distributed according to the law 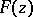 . The most commonly used examples are as follows: random numbers
. The most commonly used examples are as follows: random numbers 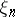 uniformly distributed on the interval
uniformly distributed on the interval  ,
, 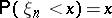 , equi-probable random binary digits
, equi-probable random binary digits 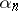 ,
, 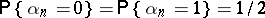 , and random normal numbers
, and random normal numbers  distributed according to the normal law with mean
distributed according to the normal law with mean  and variance 1 (cf. Uniform distribution; Normal distribution). Random numbers
and variance 1 (cf. Uniform distribution; Normal distribution). Random numbers 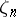 with an arbitrary distribution function
with an arbitrary distribution function 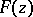 can be constructed from a sequence of uniformly-distributed random numbers
can be constructed from a sequence of uniformly-distributed random numbers 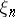 by putting
by putting  , that is, they can be found from the equation
, that is, they can be found from the equation 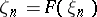 ,
, 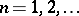 . There are also other methods of construction: for example, it is analytically simpler to obtain normally-distributed random numbers from uniformly-distributed random numbers by using the pairs
. There are also other methods of construction: for example, it is analytically simpler to obtain normally-distributed random numbers from uniformly-distributed random numbers by using the pairs
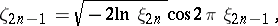 |
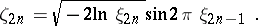 |
The digits of uniformly-distributed random numbers in binary notation are equi-probable random binary digits; conversely, by grouping equi-probable random binary digits into infinite sequences one obtains uniformly-distributed random numbers.
Random and pseudo-random numbers are used in practice in the theory of games (cf. Games, theory of), in mathematical statistics, in Monte-Carlo methods (cf. Monte-Carlo method), and in cryptography, for the concrete realization of non-determined algorithms and behaviour predicted only "on the average" . For example, if the next 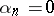 , then a player chooses the first strategy, but if
, then a player chooses the first strategy, but if  , then he/she takes the second.
, then he/she takes the second.
It is only possible to attach a strict mathematical sense to the concept of random numbers in the framework of the algorithmic probability theory of A.N. Kolmogorov [2] and P. Martin-Löf [5]. Let 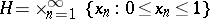 be the countably-dimensional unit hypercube, let
be the countably-dimensional unit hypercube, let 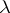 be the Lebesgue measure on
be the Lebesgue measure on 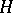 and let
and let 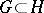 be a largest constructively-described measurable set of measure zero (it exists). Then any sequence
be a largest constructively-described measurable set of measure zero (it exists). Then any sequence  can be regarded as typical, and so taken as a sequence of uniformly-distributed random numbers. Similarly one can introduce the concept of constructive
can be regarded as typical, and so taken as a sequence of uniformly-distributed random numbers. Similarly one can introduce the concept of constructive 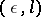 -typicality of an
-typicality of an 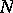 -sequence of binary symbols
-sequence of binary symbols 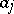 ,
,  , with respect to the system of all events
, with respect to the system of all events 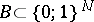 : to be of measure not more than
: to be of measure not more than  and of length of description not more than
and of length of description not more than  . It is evident from the definition that a typical sequence of uniformly-distributed random numbers cannot itself be constructive, and even the construction of an
. It is evident from the definition that a typical sequence of uniformly-distributed random numbers cannot itself be constructive, and even the construction of an 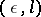 -typical sequence of random symbols requires an extraordinary large search. Therefore, in practice one uses simpler algorithms, allowing checking of their statistical "quality" with a few tests. Thus, in constructing uniformly-distributed random numbers one must necessarily test the uniform distribution of the sequence (see [3]). In simple problems, the fulfillment of certain tests can actually guarantee the usefulness of a sequence. It is sometimes more effective to use correlated random numbers, constructed from a sequence of uniformly-distributed random numbers.
-typical sequence of random symbols requires an extraordinary large search. Therefore, in practice one uses simpler algorithms, allowing checking of their statistical "quality" with a few tests. Thus, in constructing uniformly-distributed random numbers one must necessarily test the uniform distribution of the sequence (see [3]). In simple problems, the fulfillment of certain tests can actually guarantee the usefulness of a sequence. It is sometimes more effective to use correlated random numbers, constructed from a sequence of uniformly-distributed random numbers.
Tables of random numbers and random digits have been published. However, it appears to be impossible to guarantee that they satisfy all reasonable statistical tests for non-correlation.
References
| [1] | S.M. Ermakov, "Die Monte-Carlo Methode und verwandte Fragen" , Deutsch. Verlag Wissenschaft. (1975) (Translated from Russian) |
| [2] | A.N. Kolmogorov, "On tables of random numbers" Sankhya Ser. A , 25 (1963) pp. 369–376 |
| [3] | N.M. Korobov, "On some questions of uniform distribution" Izv. Akad. Nauk SSSR , 14 : 3 (1950) pp. 215–238 (In Russian) |
| [4] | D. Knuth, "The art of computer programming" , 2 , Addison-Wesley (1969) |
| [5] | P. Martin-Löf, "The definition of random sequences" Inform. and Control , 9 (1966) pp. 602–619 |
| [6] | N.N. Chentsov, "Pseudo-random numbers for simulation of Markov chains" Zh. Vychisl. Mat. i Mat. Fiz. , 7 : 3 (1967) pp. 632–643 |
| [7] | A. Shen', "Frequency approach to the definition of the notion of random sequence" Semiotika i Informatika , 18 (1982) pp. 14–42 (In Russian) |
Comments
References
| [a1] | P. Bratley, B.L. Fox, L.E. Schrage, "A guide to simulation" , Springer (1987) |
Random and pseudo-random numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Random_and_pseudo-random_numbers&oldid=14692