Distortion theorems
under conformal mapping of planar domains
Theorems characterizing the distortion of line elements at a given point of a domain, as well as the distortion of the domain and its subsets, and the distortion of the boundary of the domain under a conformal mapping. Estimates of the modulus of the derivatives of an analytic function at a point of a domain belong first of all to distortion theorems. The statement, for functions in the class 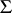 of functions
of functions
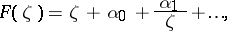 |
meromorphic and univalent in 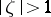 , that for all
, that for all 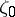 ,
, 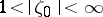 , the inequality
, the inequality
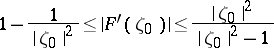 | (1) |
holds, is a distortion theorem.
Equality at the left-hand side of (1) holds only for the functions
 |
while at the right-hand side equality holds only for the functions
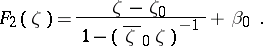 |
Here 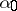 and
and 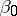 are two arbitrary fixed numbers. The functions
are two arbitrary fixed numbers. The functions 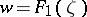 map the domain
map the domain 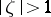 onto the
onto the 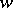 -plane with slit along the interval connecting the points
-plane with slit along the interval connecting the points 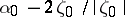 and
and 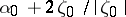 . The functions
. The functions 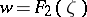 map the domain
map the domain 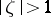 onto the
onto the 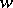 -plane with slit along an arc of the circle
-plane with slit along an arc of the circle 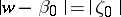 with mid-point
with mid-point 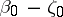 . Inequality (1) is easily obtained from the Grunsky inequality
. Inequality (1) is easily obtained from the Grunsky inequality
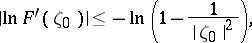 |
which determines the range of values of the functional 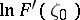 on the class
on the class 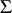 . On the other hand, inequality (1) is a direct consequence of Goluzin's theorem: If
. On the other hand, inequality (1) is a direct consequence of Goluzin's theorem: If 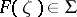 , then for any two points
, then for any two points 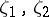 with
with 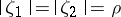 ,
, 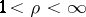 , the sharp inequality
, the sharp inequality
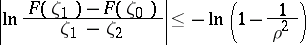 | (2) |
holds, where, moreover, the equality sign is attained for the functions 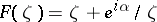 , where
, where 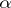 is a real constant. Inequality (2) also implies the chord-distortion theorem (cf. [1]). If
is a real constant. Inequality (2) also implies the chord-distortion theorem (cf. [1]). If 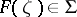 , then for any two points
, then for any two points 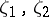 on the circle
on the circle 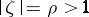 the sharp inequality
the sharp inequality
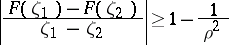 |
holds. Equality in this case is only attained for the functions
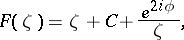 |
where 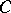 is a constant and
is a constant and 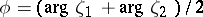 . Various generalizations of (2) are known. These give the ranges of values of corresponding functionals and are sharpened versions of distortion theorems for
. Various generalizations of (2) are known. These give the ranges of values of corresponding functionals and are sharpened versions of distortion theorems for 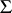 or its subclasses (cf., e.g., [1]).
or its subclasses (cf., e.g., [1]).
In the class 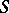 of functions
of functions
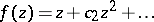 |
that are regular and univalent in the disc 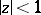 , the following sharp inequalities are valid for
, the following sharp inequalities are valid for 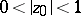 :
:
 | (3) |
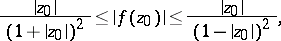 | (4) |
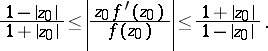 | (5) |
The estimates (4) and (5) follow from (3). The inequalities (3)–(5) are called the distortion theorems for  . The lower bounds are realized only by the functions
. The lower bounds are realized only by the functions
 |
while the upper bounds are realized only by the functions
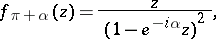 |
where 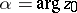 . The functions
. The functions 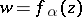 ,
, 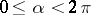 , known as the Koebe functions, map the disc
, known as the Koebe functions, map the disc 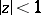 onto the
onto the 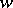 -plane with slit along the ray
-plane with slit along the ray 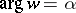 ,
, 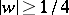 . They are extremal in a number of problems in the theory of univalent functions. Koebe's
. They are extremal in a number of problems in the theory of univalent functions. Koebe's 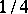 -theorem holds: The domain that is the image of the disc
-theorem holds: The domain that is the image of the disc 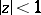 under a mapping
under a mapping 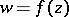 ,
,  , always contains the disc
, always contains the disc  , and the point
, and the point 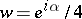 lies on the boundary of this domain only for
lies on the boundary of this domain only for 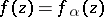 .
.
The estimates (3)–(5) are simple consequences of results on the ranges of the functionals
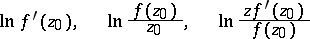 |
on  (cf. [2]).
(cf. [2]).
Let 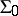 be the class of functions
be the class of functions 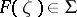 with
with 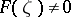 for
for 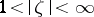 . Between functions in
. Between functions in 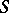 and
and 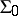 there is the following relation: If
there is the following relation: If 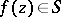 , then
, then  , and, conversely, if
, and, conversely, if 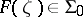 , then
, then 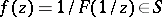 . Hence, the range of some functional (or system of functionals) on
. Hence, the range of some functional (or system of functionals) on  is determined by the range of the corresponding functional (system of functionals) on
is determined by the range of the corresponding functional (system of functionals) on  , vice versa. E.g., the range of
, vice versa. E.g., the range of 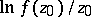 ,
, 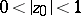 , on
, on 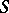 is easily obtained from that of
is easily obtained from that of 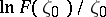 ,
, 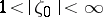 , on
, on 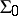 .
.
For functions that are regular and bounded in a disc, the Schwarz lemma (cf. [1]) and its generalizations, as well as the following boundary-distortion theorem of Löwner are examples of distortion theorems. Löwner's theorem: For a function  that is regular in
that is regular in 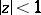 with
with 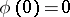 ,
, 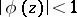 in
in 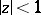 and
and 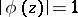 on an arc
on an arc 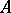 of
of  , the length of the image of
, the length of the image of 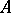 is not smaller than the length of
is not smaller than the length of 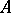 itself, and equality only holds for the functions
itself, and equality only holds for the functions 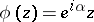 , with
, with 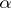 a real number.
a real number.
In the class of functions that are univalent in a given multiply-connected domain, the minimum (respectively, maximum) modulus of the derivative at a given point of the domain is attained only for mappings of this domain onto a domain with radial (resp. circular concentric) slits. For unbounded mappings the following theorem holds: Let 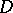 be a finitely-connected domain in the
be a finitely-connected domain in the 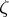 -plane containing the point at infinity, let
-plane containing the point at infinity, let 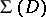 be the class of univalent functions
be the class of univalent functions 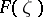 in
in 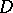 that have in a neighbourhood of
that have in a neighbourhood of 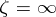 the expansion
the expansion
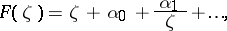 |
and let 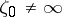 be a point in
be a point in 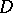 . Let
. Let 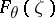 ,
, 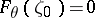 , be a function in
, be a function in 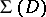 mapping
mapping 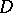 onto the plane with slits along the arcs of the logarithmic spirals that make an angle
onto the plane with slits along the arcs of the logarithmic spirals that make an angle 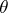 with rays emanating from the origin (it is a sufficient to take
with rays emanating from the origin (it is a sufficient to take 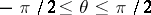 ; for
; for 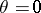 the logarithmic spiral degenerates into a ray emanating from the origin, while for
the logarithmic spiral degenerates into a ray emanating from the origin, while for 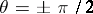 it degenerates into a circle with centre at the origin). Let
it degenerates into a circle with centre at the origin). Let
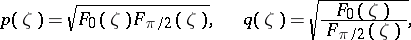 |
where those branches of the square root are taken that give first coefficients 1 in the Laurent expansions of 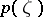 and
and 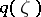 in a neighbourhood of
in a neighbourhood of 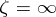 . Then the range of
. Then the range of 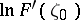 on
on 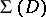 is the disc defined by
is the disc defined by
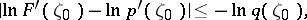 |
where to each boundary point only the functions 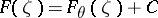 with suitable
with suitable 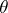 , and
, and 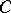 a constant, correspond. In particular, one has the sharp inequalities
a constant, correspond. In particular, one has the sharp inequalities
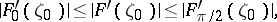 |
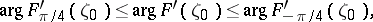 |
References
| [1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
| [3] | V.V. Chernikov, "Extremal properties of univalent conformal mappings" , Results of investigation in mathematics and mechanics during 50 years: 1917–1967 , Tomsk (1967) pp. 23–51 (In Russian) |
| [4] | I.E. Bazilevich, , Mathematics in the USSR during 40 years: 1917–1957 , 1 , Moscow (1959) pp. 444–472 (In Russian) |
| [5] | P.P. Belinskii, "General properties of quasi-conformal mappings" , Novosibirsk (1974) (In Russian) |
| [6] | R. Kühnau, "Verzerrungssätze und Koeffizientenbedingungen vom Grunskyschen Typ für quasikonforme Abbildungen" Math. Nachrichten , 48 (1971) pp. 77–105 |
Comments
Other distortion theorems are, e.g., Landau's theorems (cf. Landau theorems), Bloch's theorem (cf. Bloch constant) and the Pick theorem.
References
| [a1] | P.L. Duren, "Univalent functions" , Springer (1983) pp. Chapt. 3 |
| [a2] | C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975) |
Distortion theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distortion_theorems&oldid=14492