Quasi-isometric spaces
From Encyclopedia of Mathematics
Metric spaces (cf. Metric space) 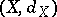 and
and 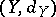 , for which there exist two mappings
, for which there exist two mappings 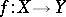 and
and 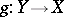 and two constants
and two constants 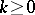 and
and 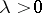 such that for all
such that for all  and
and  in
in 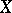 and for all
and for all 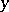 and
and 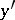 in
in 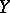 , the following four inequalities hold:
, the following four inequalities hold:
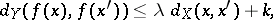 |
 |
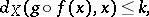 |
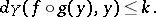 |
This definition appears in [a1], where it is attributed to G.A. Margulis. The relation "X is quasi-isometric to Y" is an equivalence relation between metric spaces.
See also Quasi-isometry.
References
| [a1] | E. Ghys, "Les groupes hyperboliques" Astérisque , 189–190 (1990) pp. 203–238 (Sém. Bourbaki Exp. 722) |
How to Cite This Entry:
Quasi-isometric spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-isometric_spaces&oldid=14441
Quasi-isometric spaces. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quasi-isometric_spaces&oldid=14441
This article was adapted from an original article by A. Papadopoulos (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article