Conway skein equivalence
From Encyclopedia of Mathematics
An equivalence relation on the set of links in 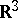 (cf. also Link). It is the smallest equivalence relation on ambient isotopy classes of oriented links, denoted by
(cf. also Link). It is the smallest equivalence relation on ambient isotopy classes of oriented links, denoted by 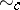 , that satisfies the following condition: If
, that satisfies the following condition: If 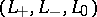 and
and 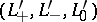 are Conway skein triples (cf. also Conway skein triple) such that if
are Conway skein triples (cf. also Conway skein triple) such that if 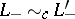 and
and  then
then 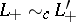 , and, furthermore, if
, and, furthermore, if 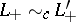 and
and 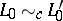 then
then 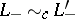 .
.
Skein equivalent links have the same Jones–Conway polynomials (cf. also Jones–Conway polynomial) and the same Murasugi signatures (for links with non-zero determinant, cf. also Signature). The last property generalizes to Tristram–Levine signatures.
References
| [a1] | J.H. Conway, "An enumeration of knots and links" J. Leech (ed.) , Computational Problems in Abstract Algebra , Pergamon (1969) pp. 329–358 |
| [a2] | C.A. Giller, "A family of links and the Conway calculus" Trans. Amer. Math. Soc. , 270 : 1 (1982) pp. 75–109 |
How to Cite This Entry:
Conway skein equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conway_skein_equivalence&oldid=14151
Conway skein equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conway_skein_equivalence&oldid=14151
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article