Chebotarev density theorem
Let 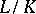 be a normal (finite-degree) extension of algebraic number fields with Galois group
be a normal (finite-degree) extension of algebraic number fields with Galois group 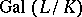 . Pick a prime ideal
. Pick a prime ideal 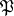 of
of 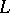 and let
and let 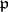 be the prime ideal of
be the prime ideal of 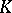 under it, i.e.
under it, i.e.  , where
, where 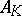 is the ring of integers of
is the ring of integers of 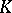 . There is a unique element
. There is a unique element
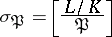 |
of 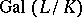 such that
such that 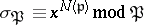 for
for 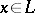 integral. Here,
integral. Here, 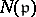 , the norm of
, the norm of 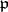 , is the number of elements of the residue field
, is the number of elements of the residue field 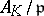 . This is the Frobenius automorphism (or Frobenius symbol) associated to
. This is the Frobenius automorphism (or Frobenius symbol) associated to 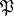 .
.
If 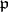 is unramified in
is unramified in  , define
, define 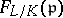 as the conjugacy class of
as the conjugacy class of 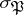 in
in  , where
, where 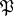 is any prime ideal above
is any prime ideal above 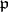 . This conjugacy class depends only on
. This conjugacy class depends only on 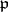 .
.
The weak form of the Chebotarev density theorem says that if 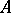 is an arbitrary conjugacy class in
is an arbitrary conjugacy class in  , then the set
, then the set
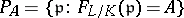 |
is infinite and has Dirichlet density 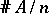 , where
, where  .
.
The stonger form specifies in addition that 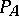 is regular (see Dirichlet density) and that
is regular (see Dirichlet density) and that
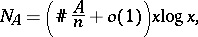 |
with 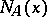 the number of prime ideals in
the number of prime ideals in 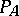 with norm
with norm 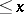 .
.
References
| [a1] | W. Narkiewicz, "Elementary and analytic theory of algebraic numbers" , PWN/Springer (1990) pp. Sect. 7.3 (Edition: Second) |
| [a2] | N.G. Chebotarev, "Determination of the density of the set of primes corresponding to a given class of permutations" Izv. Akad. Nauk. , 17 (1923) pp. 205–230; 231–250 (In Russian) |
| [a3] | N.G. Chebotarev, "Die Bestimmung der Dichtigkeit einer Menge von Primzahlen welche zu einer gegebenen Substitutionsklasse gehören" Math. Ann. , 95 (1926) pp. 191–228 |
Chebotarev density theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chebotarev_density_theorem&oldid=13409