Privileged compact set
A notion that is often used in the theory of complex spaces, in particular in the moduli theory of complex spaces. Let  be a compact Stein set in
be a compact Stein set in 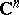 (cf. Stein manifold) and let
(cf. Stein manifold) and let  be the restriction to
be the restriction to  of the sheaf of germs of holomorphic functions in
of the sheaf of germs of holomorphic functions in 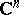 . Then
. Then  is called privileged with respect to a coherent analytic sheaf
is called privileged with respect to a coherent analytic sheaf 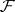 on
on 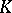 (cf. Coherent analytic sheaf) if there is an exact sequence of mappings of
(cf. Coherent analytic sheaf) if there is an exact sequence of mappings of  -sheaves
-sheaves
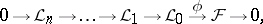 | (1) |
in which 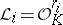 for some
for some 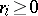 ,
, 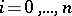 , such that the induced sequence of continuous operators
, such that the induced sequence of continuous operators
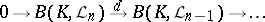 | (2) |
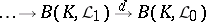 |
is exact and split (cf. Exact sequence; Split sequence). Here
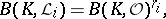 |
and 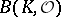 is the Banach space of continuous functions on
is the Banach space of continuous functions on 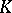 that are holomorphic in the interior of
that are holomorphic in the interior of 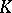 , endowed with the max-norm. Here, the sequence (2) is said to be split if the kernel and the image of the differential
, endowed with the max-norm. Here, the sequence (2) is said to be split if the kernel and the image of the differential 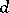 have, for every term, a direct closed complement. This condition for being split is equivalent to: There is a linear continuous operator
have, for every term, a direct closed complement. This condition for being split is equivalent to: There is a linear continuous operator 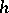 in (2) mapping
in (2) mapping 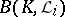 into
into 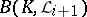 such that
such that 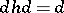 (a homotopy operator). The properties of the sequence (2) being exact and split do not depend on the choice of (1).
(a homotopy operator). The properties of the sequence (2) being exact and split do not depend on the choice of (1).
Suppose that a point  lies in the interior of
lies in the interior of 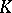 . Then there is a morphism
. Then there is a morphism 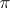 of the complex (2) into the fibre of the complex (1) over
of the complex (2) into the fibre of the complex (1) over  , mapping an element of
, mapping an element of  , i.e. a function on
, i.e. a function on  with values in
with values in 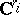 , into its germ at
, into its germ at  . This implies that the sequence
. This implies that the sequence
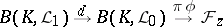 | (3) |
is semi-exact. The compact set 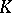 is called an
is called an 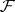 -privileged neighbourhood of
-privileged neighbourhood of  if it is an
if it is an 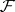 -privileged set and if (3) is an exact sequence. This property, too, does not depend on the choice of (1).
-privileged set and if (3) is an exact sequence. This property, too, does not depend on the choice of (1).
For an arbitrary coherent analytic sheaf 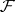 every point of its domain of definition has a fundamental system of
every point of its domain of definition has a fundamental system of 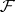 -privileged neighbourhoods. One can choose as such neighbourhoods semi-discs with certain, inequality-type, relations between the radii. There is a sufficient condition for a polycylinder to be
-privileged neighbourhoods. One can choose as such neighbourhoods semi-discs with certain, inequality-type, relations between the radii. There is a sufficient condition for a polycylinder to be 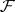 -privileged, relating the sheaf
-privileged, relating the sheaf 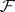 with the boundary of
with the boundary of 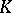 (cf. [1]).
(cf. [1]).
One also considers privileged compact sets in relation to a sheaf given on an arbitrary complex space 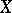 ; here one has in mind compact sets that are privileged with respect to sheaves
; here one has in mind compact sets that are privileged with respect to sheaves 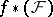 , where
, where  is a chart on
is a chart on 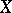 .
.
References
| [1] | A. Douady, "Le problème des modules pour les sous-espaces analytiques compacts d'un espace analytique donné" Ann. Inst. Fourier , 16 (1966) pp. 1–95 |
Privileged compact set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Privileged_compact_set&oldid=13339