Closure space
From Encyclopedia of Mathematics
Let  be a set and
be a set and  the set of subsets of
the set of subsets of  . A function
. A function  is a closure operation if for all
is a closure operation if for all  :
:
K1)  ;
;
K2)  ;
;
K3)  ;
;
K4)  ;
;
K5)  . These are the Kuratowski closure axioms, and a function
. These are the Kuratowski closure axioms, and a function  satisfying these axioms is called a Kuratowski closure operator (or Kuratowski closure operation).
satisfying these axioms is called a Kuratowski closure operator (or Kuratowski closure operation).
A pair 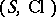 is a closure space if and only if
is a closure space if and only if  satisfies:
satisfies:
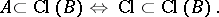 |
This condition is equivalent to K1)–K3). A closure space that satisfies K5) is a Fréchet  -space. A Fréchet
-space. A Fréchet  -space that satisfies K4) is a topological space.
-space that satisfies K4) is a topological space.
A Čech closure operator is a mapping 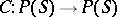 such that
such that
C1)  ;
;
C2) ( K1))
K1))  ;
;
C3)  . A set endowed with a Čech closure operator is called a pre-topological space.
. A set endowed with a Čech closure operator is called a pre-topological space.
References
| [a1] | N.M. Martin, S. Pollard, "Closure spaces and logic" , Kluwer Acad. Publ. (1996) |
| [a2] | J.L. Kelley, "General topology" , v. Nostrand–Reinhold (1955) |
| [a3] | D. Dikranjan, W. Tholin, "Categorical structures of closure operators" , Kluwer Acad. Publ. (1996) |
How to Cite This Entry:
Closure space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closure_space&oldid=13257
Closure space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closure_space&oldid=13257
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article