Birational geometry
The branch of algebraic geometry in which the main problem is the classification of algebraic varieties up to birational equivalence (cf. Birational mapping). Over a fixed field of constants  every class of birationally equivalent varieties defines a finitely generated field over
every class of birationally equivalent varieties defines a finitely generated field over 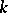 , which is isomorphic to the field of rational functions on any variety in this class. Conversely, to each such field corresponds a class of birationally equivalent varieties — the model(s) of this field. Thus, the birational classification of algebraic varieties is equivalent to the classification (up to a
, which is isomorphic to the field of rational functions on any variety in this class. Conversely, to each such field corresponds a class of birationally equivalent varieties — the model(s) of this field. Thus, the birational classification of algebraic varieties is equivalent to the classification (up to a  -isomorphism) of the finitely generated fields regular over
-isomorphism) of the finitely generated fields regular over  .
.
The most general birational invariant is the dimension of an algebraic variety. For one-dimensional algebraic varieties — irreducible algebraic curves — each class of birational equivalence contains a non-singular model — a smooth projective curve, which is unique up to 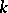 -isomorphisms. Accordingly, the birational classification of algebraic curves is reduced to the classification, up to
-isomorphisms. Accordingly, the birational classification of algebraic curves is reduced to the classification, up to  -isomorphisms, of smooth projective curves, which leads to the moduli problem. For dimensions
-isomorphisms, of smooth projective curves, which leads to the moduli problem. For dimensions  the problem becomes much more complicated. The very existence of a smooth model constitutes a problem of resolution of singularities of algebraic varieties, which at the time of writing (1986) has been positively solved only for surfaces and for varieties of arbitrary dimension over a field of characteristic zero. In such a case, if such models exist at all, there are infinitely many of them in the class of birationally equivalent varieties. The minimal models (cf. Minimal model) take a special place among such models. Their birational classification is often identical with classification up to a
the problem becomes much more complicated. The very existence of a smooth model constitutes a problem of resolution of singularities of algebraic varieties, which at the time of writing (1986) has been positively solved only for surfaces and for varieties of arbitrary dimension over a field of characteristic zero. In such a case, if such models exist at all, there are infinitely many of them in the class of birationally equivalent varieties. The minimal models (cf. Minimal model) take a special place among such models. Their birational classification is often identical with classification up to a 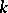 -isomorphism, as in the case of curves. However, this is not true in the general case, even for (both rational and ruled) surfaces.
-isomorphism, as in the case of curves. However, this is not true in the general case, even for (both rational and ruled) surfaces.
The principal results in the classification of algebraic surfaces were obtained by geometers of the Italian school [1]. Only isolated results are so far (1986) available [3], [7], [8] for varieties of dimensions of 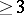 .
.
The principal discrete birational invariants of smooth complete algebraic varieties over a field 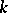 of characteristic zero include the arithmetic genus, the geometric genus, the multiple genus, the dimension of the space of regular differential forms, the Severi torsion, the fundamental group and the Brauer group.
of characteristic zero include the arithmetic genus, the geometric genus, the multiple genus, the dimension of the space of regular differential forms, the Severi torsion, the fundamental group and the Brauer group.
One of the most important problems in birational geometry is the problem of rationality of algebraic varieties, i.e. the problem of the description of rational varieties — varieties which are birationally equivalent to a projective space, cf. Rational variety.
If the field of constants is algebraically non-closed, the problems in birational geometry are closely connected with the arithmetic of algebraic varieties (cf. Algebraic varieties, arithmetic of). The important problem in such a case is that of describing the birational  -forms on a given variety
-forms on a given variety 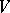 over a field
over a field 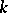 , in particular if, say,
, in particular if, say, 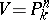 is a projective space over
is a projective space over 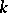 [2]. An important part of this problem is the description of the group of birational transformations of the variety
[2]. An important part of this problem is the description of the group of birational transformations of the variety 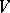 .
.
References
| [1] | "Algebraic surfaces" Trudy Mat. Inst. Steklov. , 75 (1965) (In Russian) |
| [2] | Yu.I. Manin, "Cubic forms. Algebra, geometry, arithmetic" , North-Holland (1974) (Translated from Russian) |
| [3] | L. Roth, "Algebraic threefolds" , Springer (1955) |
| [4] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [5] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [6] | I.V. Dolgachev, V.A. Iskovskikh, "The geometry of algebraic varieties" J. Soviet Math. , 5 : 6 (1976) pp. 803–864 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 12 (1974) pp. 77–170 |
| [7] | J. Soviet Math. , 13 : 6 (1980) Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 12 (1979) |
| [8] | S. Iitaka, "Algebraic geometry, an introduction to birational geometry of algebraic varieties" , Springer (1982) |
| [9] | R. Hartshorne, "Algebraic geometry" , Springer (1977) |
Comments
A field extension 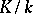 is regular if
is regular if 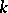 is algebraically closed in
is algebraically closed in  and
and 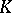 is linearly disjoint from the algebraic closure
is linearly disjoint from the algebraic closure 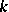 of
of  over
over 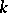 . If
. If 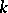 is algebraically closed, then every extension of
is algebraically closed, then every extension of 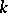 is regular and there is an arrow-reversing equivalence of categories between the category of varieties and dominant rational mappings over
is regular and there is an arrow-reversing equivalence of categories between the category of varieties and dominant rational mappings over 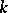 and the category of finitely generated field extensions, cf. [8], Sect. I.4. For dimension
and the category of finitely generated field extensions, cf. [8], Sect. I.4. For dimension  many new results have recently become available in the (birational) classification of algebraic varieties, cf. [a1].
many new results have recently become available in the (birational) classification of algebraic varieties, cf. [a1].
References
| [a1] | A. Conte (ed.) , Algebraic threefolds , Lect. notes in math. , 947 , Springer (1982) |
Birational geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Birational_geometry&oldid=12684