Lagrange theorem
For Lagrange's theorem in differential calculus see Finite-increments formula.
Lagrange's theorem in group theory: The order 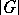 of any finite group
of any finite group 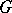 is divisible by the order
is divisible by the order  of any subgroup
of any subgroup 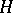 of it. The theorem was actually proved by J.L. Lagrange in 1771 in the study of properties of permutations in connection with research on the solvability of algebraic equations in radicals.
of it. The theorem was actually proved by J.L. Lagrange in 1771 in the study of properties of permutations in connection with research on the solvability of algebraic equations in radicals.
References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) |
Comments
References
| [a1] | P. Hall, "The theory of groups" , Macmillan (1959) pp. Chapt. 10 |
| [a2] | B.L. van der Waerden, "Algebra" , 2 , Springer (1967) (Translated from German) |
Lagrange's theorem on congruences: The number of solutions of the congruence
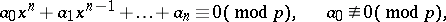 |
modulo a prime number 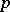 does not exceed its degree
does not exceed its degree  . This was proved by J.L. Lagrange (see [1]). It can be generalized to polynomials with coefficients from an arbitrary integral domain.
. This was proved by J.L. Lagrange (see [1]). It can be generalized to polynomials with coefficients from an arbitrary integral domain.
References
| [1] | J.L. Lagrange, "Nouvelle méthode pour résoudre les problèmes indéterminés en nombres entièrs" J.A. Serret (ed.) , Oeuvres , 2 , G. Olms, reprint (1973) pp. 653–726 |
| [2] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
S.A. Stepanov
Comments
References
| [a1] | B.L. van der Waerden, "Algebra" , 2 , Springer (1971) (Translated from German) |
Lagrange's theorem on the sum of four squares: Any natural number can be represented as the sum of four squares of integers. This was established by J.L. Lagrange [1]. For a generalization of Lagrange's theorem see Waring problem.
References
| [1] | J.L. Lagrange, "Démonstration d'un théorème d'arithmétique" J.A. Serret (ed.) , Oeuvres , 3 , G. Olms, reprint (1973) pp. 187–201 |
| [2] | J.-P. Serre, "A course in arithmetic" , Springer (1973) (Translated from French) |
S.M. Voronin
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 23 |
Lagrange's theorem on continued fractions: Any continued fraction that represents a quadratic irrationality is periodic. This was established by J.L. Lagrange [1].
References
| [1] | J.L. Lagrange, "Sur la solution des problèmes indéterminés du second degré" J.A. Serret (ed.) , Oeuvres , 2 , G. Olms, reprint (1973) pp. 376–535 |
| [2] | A.Ya. Khinchin, "Continued fractions" , Univ. Chicago Press (1964) pp. Chapt. II, §10 (Translated from Russian) |
S.M. Voronin
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. 23 |
Lagrange theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lagrange_theorem&oldid=12018