Fractal dimension
From Encyclopedia of Mathematics
A, possibly non-integer valued, dimension concept. Let 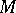 be a metric space and
be a metric space and 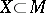 a bounded subset. For each
a bounded subset. For each  let
let 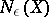 be the minimal number of balls of radius
be the minimal number of balls of radius  necessary to cover
necessary to cover 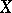 . Then
. Then
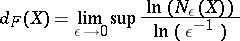 |
is the fractal dimension of 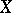 . It has also been called the capacity, the Mandelbrot dimension or the Shnirel'man–Kolmogorov dimension of
. It has also been called the capacity, the Mandelbrot dimension or the Shnirel'man–Kolmogorov dimension of 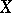 .
.
One has
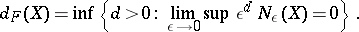 |
If 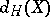 denotes the Hausdorff dimension of
denotes the Hausdorff dimension of 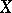 , then
, then 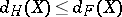 .
.
References
| [a1] | B.B. Mandelbrot, "Form, chance and dimension" , Freeman (1977) |
How to Cite This Entry:
Fractal dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractal_dimension&oldid=11902
Fractal dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractal_dimension&oldid=11902