Normal sub-semi-group
From Encyclopedia of Mathematics
of a semi-group 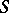
A sub-semi-group 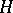 satisfying the following condition: For any
satisfying the following condition: For any 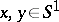 (for the notation
(for the notation 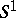 see Normal complex) such that
see Normal complex) such that 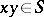 and for any
and for any 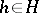 the relations
the relations 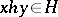 and
and 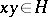 are equivalent. A subset of
are equivalent. A subset of 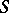 is a normal sub-semi-group if and only if it is the complete inverse image of the unit element under some homomorphism of
is a normal sub-semi-group if and only if it is the complete inverse image of the unit element under some homomorphism of 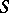 onto a semi-group with unit element.
onto a semi-group with unit element.
References
| [1] | E.S. Lyapin, "Semigroups" , Amer. Math. Soc. (1974) (Translated from Russian) |
How to Cite This Entry:
Normal sub-semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_sub-semi-group&oldid=11415
Normal sub-semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_sub-semi-group&oldid=11415
This article was adapted from an original article by L.N. Shevrin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article