Multiple comparison
The problem of testing hypotheses with respect to the values of scalar products  of a vector
of a vector 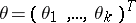 , the coordinates of which are unknown parameters, with a number of given vectors
, the coordinates of which are unknown parameters, with a number of given vectors 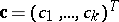 . In statistical research the multiple comparison problem often arises in dispersion analysis where, as a rule, the vectors
. In statistical research the multiple comparison problem often arises in dispersion analysis where, as a rule, the vectors  are chosen so that
are chosen so that 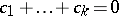 , and the scalar product
, and the scalar product 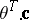 itself, in this case, is called a contrast. On the assumption that
itself, in this case, is called a contrast. On the assumption that  are unknown mathematical expectations of one-dimensional normal laws, J.W. Tukey and H. Scheffé proposed the
are unknown mathematical expectations of one-dimensional normal laws, J.W. Tukey and H. Scheffé proposed the  -method and the
-method and the 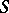 -method, respectively, for the simultaneous estimation of contrasts, which are the fundamental methods in the problem of constructing confidence intervals for contrasts.
-method, respectively, for the simultaneous estimation of contrasts, which are the fundamental methods in the problem of constructing confidence intervals for contrasts.
References
| [1] | H. Scheffé, "The analysis of variance" , Wiley (1959) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 3. Design and analysis, and time series , Griffin (1983) |
Comments
References
| [a1] | R. Miller, "Simultaneous statistical inference" , McGraw-Hill (1966) |
Multiple comparison. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiple_comparison&oldid=11413