Quadratic irrationality
From Encyclopedia of Mathematics
A root of a quadratic trinomial with rational coefficients which is irreducible over the field of rational numbers. A quadratic irrationality is representable in the form 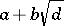 , where
, where  and
and 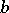 are rational numbers,
are rational numbers, 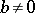 , and
, and 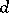 is an integer which is not a perfect square. A real number
is an integer which is not a perfect square. A real number 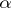 is a quadratic irrationality if and only if it has an infinite periodic continued fraction expansion.
is a quadratic irrationality if and only if it has an infinite periodic continued fraction expansion.
Comments
References
| [a1] | A.Ya. Khinchin, "Continued fractions" , Phoenix Sci. Press (1964) pp. Chapt. II, §10 (Translated from Russian) |
How to Cite This Entry:
Quadratic irrationality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadratic_irrationality&oldid=11391
Quadratic irrationality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quadratic_irrationality&oldid=11391
This article was adapted from an original article by A.I. Galochkin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article