Baker-Beynon duality
The free Riesz space on  generators,
generators, 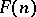 , may be described as follows: View the set of all real-valued functions on
, may be described as follows: View the set of all real-valued functions on 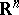 as a Riesz space under the pointwise operations. Then
as a Riesz space under the pointwise operations. Then 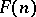 may be identified with the Riesz subspace generated by the
may be identified with the Riesz subspace generated by the  coordinate projections
coordinate projections 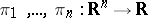 . This follows from universal algebra and the fact that
. This follows from universal algebra and the fact that 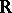 generates an equational class of Riesz spaces, see [a4], p. 355. The elements of
generates an equational class of Riesz spaces, see [a4], p. 355. The elements of 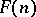 are continuous functions that are piecewise-homogeneous linear in polyhedral cones with common vertex
are continuous functions that are piecewise-homogeneous linear in polyhedral cones with common vertex 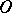 .
.
If 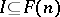 is a Riesz ideal, let
is a Riesz ideal, let
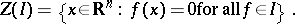 |
If 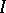 is finitely generated and
is finitely generated and 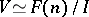 , then
, then 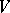 is said to be finitely presentable. In this case,
is said to be finitely presentable. In this case, 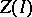 is a polyhedral cone (with vertex
is a polyhedral cone (with vertex 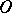 ) and
) and 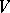 is isomorphic to the Riesz space of all piecewise-homogeneous linear functions on
is isomorphic to the Riesz space of all piecewise-homogeneous linear functions on 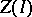 . Much of this can be found in [a1], but the crucial observation that all piecewise-homogeneous linear functions occur appears first in [a2]. Baker–Beynon duality [a3] states that the category
. Much of this can be found in [a1], but the crucial observation that all piecewise-homogeneous linear functions occur appears first in [a2]. Baker–Beynon duality [a3] states that the category 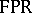 of finitely presentable Riesz spaces and arbitrary Riesz homomorphisms is dually equivalent to the category
of finitely presentable Riesz spaces and arbitrary Riesz homomorphisms is dually equivalent to the category 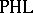 of polyhedral cones (with vertex at
of polyhedral cones (with vertex at 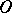 ) in some
) in some 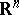 and with piecewise-homogeneous linear morphisms. The equivalence is via enriched
and with piecewise-homogeneous linear morphisms. The equivalence is via enriched 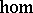 -functors. For any object
-functors. For any object 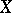 of
of 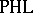 ,
, 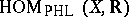 inherits the structure of a Riesz space from
inherits the structure of a Riesz space from 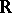 . In the other direction, if
. In the other direction, if 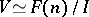 is in
is in 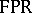 , then
, then 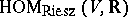 is in one-to-one correspondence with
is in one-to-one correspondence with 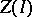 .
.
It can be shown that if also 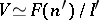 , then
, then 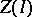 and
and 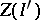 are
are 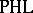 -equivalent. There is an induced duality between the category of finitely presentable Riesz spaces with a distinguished strong unit and unit-preserving morphisms and the familiar category
-equivalent. There is an induced duality between the category of finitely presentable Riesz spaces with a distinguished strong unit and unit-preserving morphisms and the familiar category 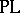 of polyhedra and piecewise-affine linear mappings, [a3].
of polyhedra and piecewise-affine linear mappings, [a3].
Among the first applications of this theory is Baker's proof [a1] that the finitely generated projectives in the category of Riesz spaces are precisely the finitely presented Riesz spaces. This corresponds to the peculiar feature of 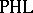 that every object is an absolute retract (cf. also Collapsibility). Presently (1996), nothing significant is known about projectives that are not finitely generated.
that every object is an absolute retract (cf. also Collapsibility). Presently (1996), nothing significant is known about projectives that are not finitely generated.
For important recent work related to Abelian 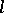 -groups (cf.
-groups (cf. 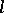 -group), see [a5].
-group), see [a5].
References
| [a1] | K.A. Baker, "Free vector lattices" Canadian J. Math. , 20 (1968) pp. 58–66 |
| [a2] | W.M. Beynon, "Combinatorial aspects of piecewise linear functions" J. London Math. Soc. , 7 (1974) pp. 719–727 |
| [a3] | W.M. Beynon, "Duality theorems for finitely generated vector lattices" Proc. London Math. Soc. , 31 (1975) pp. 114–128 |
| [a4] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , Amer. Math. Soc. (1967) (Edition: Third) |
| [a5] | D. Mundici, "Farey stellar subdivisions, ultrasimplicial groups and 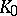 of AF of AF 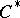 -algebras" Adv. Math. , 68 (1988) pp. 23–39 -algebras" Adv. Math. , 68 (1988) pp. 23–39 |
Baker-Beynon duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baker-Beynon_duality&oldid=11389