Probability measure
probability distribution, probability
A real non-negative function 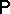 on a class
on a class 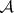 of subsets (events) of a non-empty set
of subsets (events) of a non-empty set  (the space of elementary events) forming a
(the space of elementary events) forming a 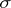 -field (i.e. a set closed with respect to countable set-theoretic operations) such that
-field (i.e. a set closed with respect to countable set-theoretic operations) such that
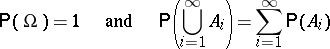 |
if 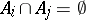 for
for 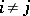 (
(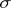 -additivity).
-additivity).
Examples of probability measures.
1) 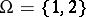 ;
; 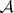 is the class of all subsets of
is the class of all subsets of  ;
; 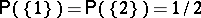 (this probability measure corresponds to a random experiment consisting in throwing a symmetrical coin; if heads correspond to 1 while tails correspond to 2, the probability of throwing heads (tails) is 1/2);
(this probability measure corresponds to a random experiment consisting in throwing a symmetrical coin; if heads correspond to 1 while tails correspond to 2, the probability of throwing heads (tails) is 1/2);
2)  ;
; 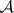 is the class of all subsets of
is the class of all subsets of  ;
;
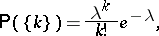 |
where 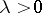 (the Poisson distribution);
(the Poisson distribution);
3) 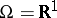 ;
; 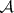 is the class of Borel subsets of
is the class of Borel subsets of 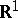 ;
;
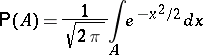 |
(the normal distribution);
4) 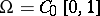 is the space of continuous real functions
is the space of continuous real functions 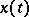 on
on  that vanish at the point zero;
that vanish at the point zero; 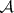 is the class of Borel subsets with respect to the topology of uniform convergence;
is the class of Borel subsets with respect to the topology of uniform convergence; 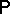 is the measure which is uniquely defined by the formula
is the measure which is uniquely defined by the formula
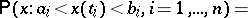 |
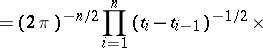 |
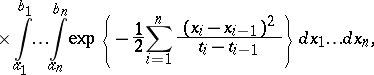 |
where  is an arbitrary natural number and
is an arbitrary natural number and 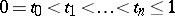 (the Wiener measure).
(the Wiener measure).
References
| [1] | A.N. Kolmogorov, "Foundations of the theory of probability" , Chelsea, reprint (1950) (Translated from Russian) |
| [2] | B.V. Gnedenko, "The theory of probability" , Chelsea, reprint (1962) (Translated from Russian) |
Comments
References
| [a1] | P. Billingsley, "Probability and measure" , Wiley (1979) |
Probability measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Probability_measure&oldid=11376