Sinusoidal spiral
A plane curve whose equation in polar coordinates has the form
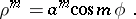 |
When 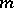 is rational, this is an algebraic curve. In particular, when
is rational, this is an algebraic curve. In particular, when 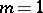 it is a circle, when
it is a circle, when 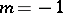 — an equilateral hyperbola, when
— an equilateral hyperbola, when 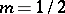 — a cardioid, and when
— a cardioid, and when 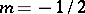 — a parabola.
— a parabola.
For general 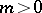 the sinusoidal spiral passes through the pole, and is entirely contained within a circle of radius
the sinusoidal spiral passes through the pole, and is entirely contained within a circle of radius  . When
. When 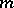 is negative, the radius vector of the curve can take arbitrarily large values and the curve does not pass through the pole. The sinusoidal spiral is symmetric with respect to the polar axis, and when
is negative, the radius vector of the curve can take arbitrarily large values and the curve does not pass through the pole. The sinusoidal spiral is symmetric with respect to the polar axis, and when 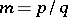 is rational (where
is rational (where 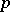 and
and 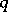 are relatively prime numbers), it has
are relatively prime numbers), it has 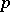 axes of symmetry passing through the pole. When
axes of symmetry passing through the pole. When 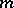 is a positive integer, the radius vector of the curve is a periodic function of period
is a positive integer, the radius vector of the curve is a periodic function of period 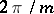 . As
. As 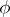 goes from 0 to
goes from 0 to 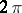 , the curve consists of
, the curve consists of 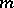 branches, each contained in an angle of
branches, each contained in an angle of 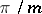 . In this case the pole is a multiple point (see Fig.). When
. In this case the pole is a multiple point (see Fig.). When 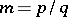 is a positive rational number, the curve consists of
is a positive rational number, the curve consists of 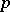 intersecting branches. When
intersecting branches. When 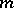 is a negative integer, the curve consists of
is a negative integer, the curve consists of 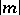 infinite branches, which can be obtained by inverting the spiral with
infinite branches, which can be obtained by inverting the spiral with 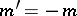 .
.
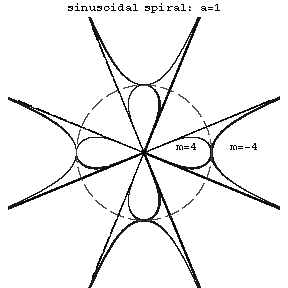
Figure: s085650a
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
Comments
References
| [a1] | E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1967) |
Sinusoidal spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sinusoidal_spiral&oldid=11361