Bochner integral
An integral of a function with values in a Banach space with respect to a scalar measure. It belongs to the so-called strong integrals (cf. Strong integral).
Let 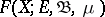 be the vector space of functions
be the vector space of functions 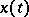 ,
, 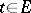 , with values in a Banach space
, with values in a Banach space 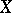 , given on a space
, given on a space 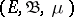 with a countably-additive scalar measure
with a countably-additive scalar measure 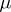 on a
on a 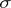 -algebra
-algebra 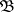 of subsets of
of subsets of 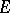 . A function
. A function 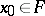 is called simple if
is called simple if
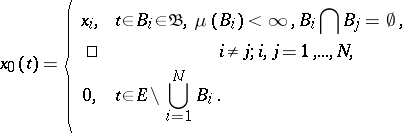 |
A function 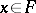 is called strongly measurable if there exists a sequence
is called strongly measurable if there exists a sequence 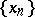 of simple functions with
of simple functions with 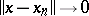 almost-everywhere with respect to the measure
almost-everywhere with respect to the measure 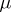 on
on 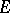 . In such a case the scalar function
. In such a case the scalar function 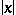 is
is 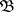 -measurable. For the simple function
-measurable. For the simple function 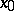
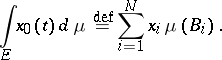 |
A function  is said to be Bochner integrable if it is strongly measurable and if for some approximating sequence
is said to be Bochner integrable if it is strongly measurable and if for some approximating sequence 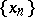 of simple functions
of simple functions
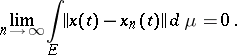 |
The Bochner integral of such a function over a set 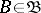 is
is
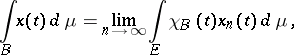 |
where 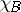 is the characteristic function of
is the characteristic function of 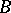 , and the limit is understood in the sense of strong convergence in
, and the limit is understood in the sense of strong convergence in 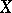 . This limit exists, and is independent of the choice of the approximation sequence of simple functions.
. This limit exists, and is independent of the choice of the approximation sequence of simple functions.
Criterion for Bochner integrability: For a strongly-measurable function 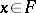 to be Bochner integrable it is necessary and sufficient for the norm of this function to be integrable, i.e.
to be Bochner integrable it is necessary and sufficient for the norm of this function to be integrable, i.e.
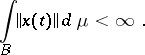 |
The set of Bochner-integrable functions forms a vector subspace 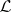 of
of 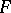 , and the Bochner integral is a linear operator on this subspace.
, and the Bochner integral is a linear operator on this subspace.
Properties of Bochner integrals:
1)
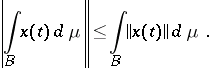 |
2) A Bochner integral is a countably-additive 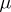 -absolutely continuous set-function on the
-absolutely continuous set-function on the 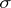 -algebra
-algebra 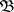 , i.e.
, i.e.
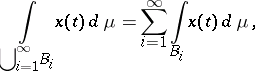 |
if 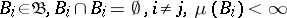 , and
, and 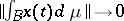 if
if 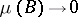 , uniformly for
, uniformly for 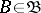 .
.
3) If 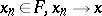 almost-everywhere with respect to the measure
almost-everywhere with respect to the measure 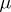 on
on 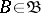 , if
, if 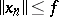 almost-everywhere with respect to
almost-everywhere with respect to 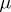 on
on 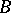 , and if
, and if 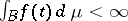 , then
, then
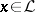 |
and
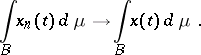 |
4) The space 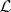 is complete with respect to the norm (cf. Convergence in norm)
is complete with respect to the norm (cf. Convergence in norm)
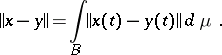 |
5) If 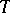 is a closed linear operator from a Banach space
is a closed linear operator from a Banach space 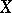 into a Banach space
into a Banach space 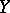 and if
and if
 |
then
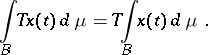 |
If 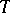 is bounded, the condition
is bounded, the condition
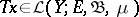 |
is automatically fulfilled, [3]–[5].
The Bochner integral was introduced by S. Bochner [1]. Equivalent definitions were given by T. Hildebrandt [2] and N. Dunford (the 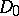 -integral).
-integral).
References
| [1] | S. Bochner, "Integration von Funktionen, deren Werte die Elemente eines Vektorraumes sind" Fund. Math. , 20 (1933) pp. 262–276 |
| [2] | T.H. Hildebrandt, "Integration in abstract spaces" Bull. Amer. Math. Soc. , 59 (1953) pp. 111–139 |
| [3] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 |
| [4] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
| [5] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
Comments
A simple function is also called a step function. A good recent textbook on integrals with values in a Banach space is [a1]; [a4] is specifically about the Bochner integral.
References
| [a1] | J. Diestel, J.J. Uhl jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977) |
| [a2] | A.C. Zaanen, "Integration" , North-Holland (1967) |
| [a3] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [a4] | J. Mikusiński, "The Bochner integral" , Acad. Press (1978) |
Bochner integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bochner_integral&oldid=11334