Biorthogonal system
A pair of sets 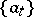 and
and 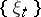 ,
, 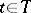 , of elements of a (topological) vector space
, of elements of a (topological) vector space 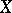 and the dual (topological) space
and the dual (topological) space 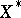 , respectively, which satisfies the conditions
, respectively, which satisfies the conditions
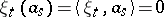 |
if 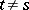 , and
, and 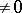 if
if 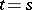 (here,
(here, 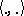 is the canonical bilinear form coupling
is the canonical bilinear form coupling 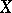 and
and 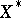 ). For instance, a biorthogonal system consists of a Schauder basis and the set formed by the expansion coefficients of
). For instance, a biorthogonal system consists of a Schauder basis and the set formed by the expansion coefficients of  in it. In a Hilbert space
in it. In a Hilbert space 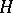 with scalar product
with scalar product 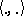 and basis
and basis 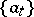 the set
the set 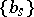 satisfying the condition
satisfying the condition
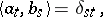 |
where 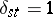 if
if 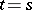 and
and 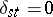 if
if 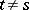 , is also a basis; it is said to be the basis dual to
, is also a basis; it is said to be the basis dual to 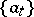 and, since
and, since 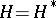 , the sets
, the sets 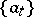 and
and 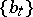 form a biorthogonal system. In particular, a basis in
form a biorthogonal system. In particular, a basis in 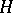 is said to be orthonormal if its dual to itself.
is said to be orthonormal if its dual to itself.
However, there also exist biorthogonal systems which do not even form a weak basis; an example is the set of functions 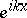 ,
, 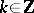 ,
, 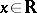 , in the space of continuous periodic functions with the norm
, in the space of continuous periodic functions with the norm 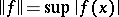 .
.
Biorthogonal system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Biorthogonal_system&oldid=11290