Stress tensor
A tensor defining the distribution of internal stresses in a body under strain. The stress tensor is a symmetric tensor 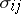 of rank 2. The component
of rank 2. The component  is the
is the  -th component of the force acting on a unit surface perpendicular to the
-th component of the force acting on a unit surface perpendicular to the 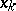 -axis. Thus, acting on a unit area perpendicular to the
-axis. Thus, acting on a unit area perpendicular to the  -axis, one has a normal stress
-axis, one has a normal stress 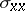 (i.e. a force in the direction of the
(i.e. a force in the direction of the  -axis) and shearing stresses (i.e. forces in the directions of the
-axis) and shearing stresses (i.e. forces in the directions of the  - and
- and  -axes)
-axes) 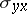 and
and 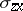 . The stressed state defined by the components of the stress tensor can be resolved into two stressed states. The first is that characterized by the isotropic stress tensor:
. The stressed state defined by the components of the stress tensor can be resolved into two stressed states. The first is that characterized by the isotropic stress tensor:
 |
with 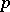 the hydrostatic pressure.
the hydrostatic pressure.
The second stressed state is characterized by the components of the deviatoric stress tensor:
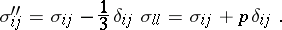 |
References
| [1] | L.D. Landau, E.M. Lifshitz, "Elasticity theory" , Pergamon (1959) (Translated from Russian) |
Comments
In general continuum theory, the stress tensor is not necessarily symmetric. The symmetry is lost when coupled stresses are present (polar materials).
References
| [a1] | C. Truesdell, W. Noll, "The non-linear field theories of mechanics" S. Flügge (ed.) , Handbuch der Physik , III/3 , Springer (1965) pp. 1–602 |
| [a2] | C. Truesdell, R. Toupin, "The classical field theories" S. Flügge (ed.) , Handbuch der Physik , III/1 , Springer (1960) pp. 226–793 |
| [a3] | I.S. [I.S. Sokolnikov] Sokolnikoff, "Mathematical theory of elasticity" , McGraw-Hill (1956) (Translated from Russian) |
Stress tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stress_tensor&oldid=11269