Game with a hierarchy structure
A model of a conflict situation with a fixed sequence of moves and interchange of information between the players. The main object of investigation in the theory of games with a hierarchy structure is the problem of finding the largest guaranteed result and an optimal strategy for a selected player. Suppose that players 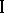 and
and 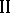 , respectively, tend to an increase in the pay-off functions
, respectively, tend to an increase in the pay-off functions  and
and 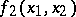 (cf. Gain function), continuous on the product of two compacta
(cf. Gain function), continuous on the product of two compacta 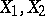 ;
; 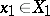 ,
, 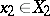 . The following different types of games can be formulated according to the character of the information and the order of moves.
. The following different types of games can be formulated according to the character of the information and the order of moves.
The game  . Player
. Player 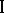 chooses
chooses 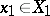 and communicates his choice to player
and communicates his choice to player  . Let
. Let
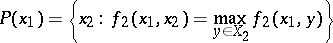 |
be the set of optimal choices of player 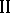 . Then the largest guaranteed result for player
. Then the largest guaranteed result for player 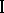 is
is
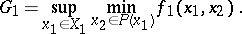 |
The game 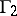 . Player
. Player  expects to have and indeed will have information on the choices of player
expects to have and indeed will have information on the choices of player 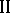 ; he communicates his strategy, that is, a function
; he communicates his strategy, that is, a function 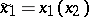 , where
, where 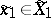 — the set of all mappings from
— the set of all mappings from 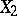 to
to 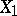 , to player
, to player  . The largest guaranteed result for player
. The largest guaranteed result for player 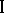 is
is
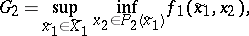 |
where the set of optimal choices of player 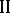 is
is
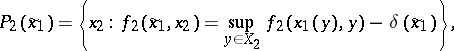 |
where 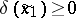 , and
, and 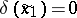 if and only if
if and only if 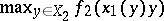 is achieved.
is achieved.
The game 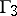 . Player
. Player 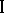 expects to have and indeed will have information on the choices of player
expects to have and indeed will have information on the choices of player 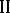 in the form
in the form 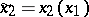 , where
, where 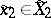 — the set of all mappings from
— the set of all mappings from 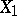 to
to  ; he communicates to player
; he communicates to player 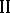 his strategy
his strategy 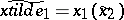 , where
, where 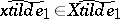 — the set of mappings from
— the set of mappings from 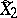 to
to 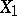 . The largest guaranteed result of player
. The largest guaranteed result of player 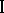 is
is
 |
where
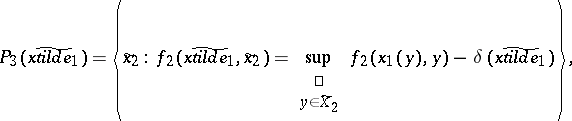 |
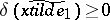 , where now
, where now 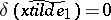 if and only if
if and only if 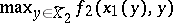 is achieved.
is achieved.
A relation between the results in these games determines for player 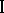 knowledge of the information concerning the actions of player II:
knowledge of the information concerning the actions of player II: 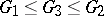 . Using the scheme indicated in the construction of the strategies of the players, games with arbitrarily deep recursion can be formulated. The following assertion holds: in the games
. Using the scheme indicated in the construction of the strategies of the players, games with arbitrarily deep recursion can be formulated. The following assertion holds: in the games 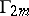 ,
,  , the largest guaranteed result for player
, the largest guaranteed result for player  is
is 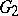 ; in the games
; in the games 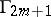 ,
, 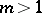 , the largest guaranteed result is
, the largest guaranteed result is 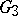 . The problem of determining
. The problem of determining 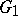 is related to a class of problems of minimax type with related restrictions.
is related to a class of problems of minimax type with related restrictions.
Methods have been developed for solving 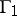 using penalty functions, necessary optimality conditions and approximation to the original game by games with unique responses for player
using penalty functions, necessary optimality conditions and approximation to the original game by games with unique responses for player 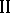 . Complete solutions are known for special classes of games: games with close interests, bimatrix games, bilinear games, etc. The problem of determining
. Complete solutions are known for special classes of games: games with close interests, bimatrix games, bilinear games, etc. The problem of determining 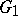 is not well-posed relative to changes in the function
is not well-posed relative to changes in the function 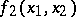 in the uniform metric and of the sets
in the uniform metric and of the sets 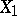 and
and 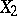 in the Hausdorff metric. A general method has been proposed for regularizing the solution of the game
in the Hausdorff metric. A general method has been proposed for regularizing the solution of the game 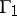 ; regularization of the problem relative to the pay-off function of
; regularization of the problem relative to the pay-off function of 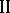 is effected at the expense of introducing an artificial inaccuracy in the determination of
is effected at the expense of introducing an artificial inaccuracy in the determination of 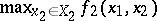 . The determination of the magnitude
. The determination of the magnitude  reduces to the solution of a set of problems in mathematical programming.
reduces to the solution of a set of problems in mathematical programming.
Suppose that for arbitrary 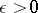 the following functions, sets and numbers are defined:
the following functions, sets and numbers are defined:
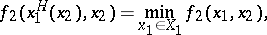 |
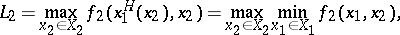 |
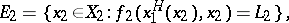 |
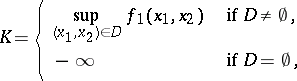 |
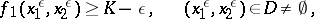 |
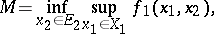 |
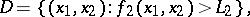 |
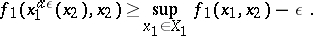 |
Under the conditions stated, 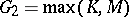 and the strategy
and the strategy
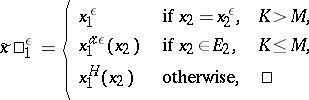 |
guarantees that player 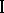 receives
receives 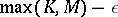 for sufficiently small
for sufficiently small  . As is clear from the definitions, an optimal strategy consists of a certain number of stages, the last playing the part of a strategy by punishment.
. As is clear from the definitions, an optimal strategy consists of a certain number of stages, the last playing the part of a strategy by punishment.
If 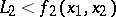 and if
and if 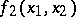 has no local maxima with value
has no local maxima with value 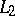 on
on 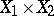 , then
, then 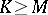 and an optimal strategy has the simple form:
and an optimal strategy has the simple form:
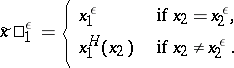 |
A solution can be found in a similar way for 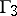 ; it also reduces to the solution of a sequence of problems in mathematical programming.
; it also reduces to the solution of a sequence of problems in mathematical programming.
When side payments for player 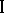 are introduced into a game with a hierarchy structure as functions of the choices of player
are introduced into a game with a hierarchy structure as functions of the choices of player 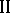 , the expression for the largest guaranteed result for player
, the expression for the largest guaranteed result for player  is significantly simplified. In the game
is significantly simplified. In the game 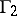 , where
, where
 |
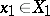 ,
, 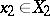 ,
, 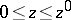 , and player
, and player 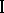 chooses strategies
chooses strategies 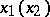 ,
, 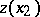 , the determination of
, the determination of 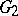 reduces to the solution of a problem in mathematical programming:
reduces to the solution of a problem in mathematical programming:
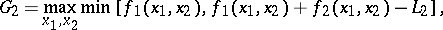 |
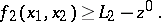 |
In general, the application of arbitrarily small side payments 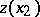 in games with a hierarchy structure allows player
in games with a hierarchy structure allows player  to achieve the largest possible guaranteed result, reckoning on the generosity of his partner.
to achieve the largest possible guaranteed result, reckoning on the generosity of his partner.
The games formulated can be generalized to the case of step-by-step receipt and use of information in a dynamical way. In the case where the states of the players are described by differential or difference equations there arises an extensive class of problems connected with the diversity of the forms of the players' information on the state and trend as a physical process as well as a process of making a decision. Generalizations of the games 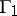 and
and 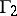 are considered to the case of prohibited situations, that is, the presence of joint restrictions on the players' choices.
are considered to the case of prohibited situations, that is, the presence of joint restrictions on the players' choices.
The formulations mentioned relate to the case where player 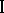 has complete information on the pay-off function and the set of his choices. If player
has complete information on the pay-off function and the set of his choices. If player 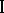 knows that the continuous pay-off function of
knows that the continuous pay-off function of  satisfies the inequalities
satisfies the inequalities
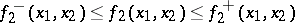 |
for known continuous functions 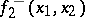 and
and 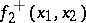 , then the largest guaranteed result in
, then the largest guaranteed result in  is defined by maximizing conditions for a function of a single variable.
is defined by maximizing conditions for a function of a single variable.
A more general version of the case where player 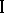 has incomplete information of the interests of player
has incomplete information of the interests of player  is as follows. Player
is as follows. Player 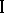 knows the function
knows the function 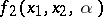 ,
,  , and knows that the true pay-off function satisfies
, and knows that the true pay-off function satisfies 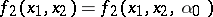 for some unknown value
for some unknown value 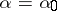 . With such information, the solution of
. With such information, the solution of 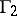 for finite sets
for finite sets 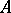 reduces to maximizing functions of several variables; for infinite
reduces to maximizing functions of several variables; for infinite  the problem is more complicated. The presence of indefinite factors in the formulation of
the problem is more complicated. The presence of indefinite factors in the formulation of 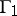 does not lead to a significant complication of the problem, since this case reduces to that of a case without indefiniteness. In the indefinite case of
does not lead to a significant complication of the problem, since this case reduces to that of a case without indefiniteness. In the indefinite case of 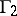 , a number of problems are considered, where the concept of a players' strategy is extended at the expense of the hypothesis that player
, a number of problems are considered, where the concept of a players' strategy is extended at the expense of the hypothesis that player 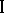 communicates his effectiveness criterion to player
communicates his effectiveness criterion to player 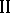 , that is, some
, that is, some 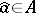 , so that the final choice
, so that the final choice 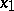 can be performed by obtaining information about
can be performed by obtaining information about 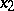 and the effectiveness criterion of player
and the effectiveness criterion of player 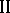 . If player
. If player 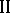 is cautious in the case, that is, he holds to the principle of the largest guaranteed result, and player
is cautious in the case, that is, he holds to the principle of the largest guaranteed result, and player 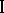 communicates to him the parametrized strategy
communicates to him the parametrized strategy 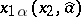 ,
, 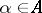 , then it can be shown that the largest guaranteed result of player
, then it can be shown that the largest guaranteed result of player 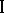 is
is 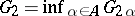 , where
, where 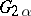 is the largest guaranteed result of player
is the largest guaranteed result of player  in the game
in the game 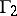 for a given
for a given 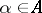 . A similar result holds without assuming that player
. A similar result holds without assuming that player  is cautious, if player
is cautious, if player  knows a parametric family of sets
knows a parametric family of sets 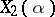 ,
, 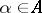 , one of which is the true one.
, one of which is the true one.
Close to the problem just discussed is that of finding the largest guaranteed result of player 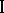 in
in  in the presence of a parameter
in the presence of a parameter 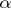 in the pay-off functions of the players characterizing environmental uncertainty, where player
in the pay-off functions of the players characterizing environmental uncertainty, where player 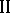 is informed by his choice of the concrete value of
is informed by his choice of the concrete value of  and player
and player 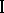 is not informed.
is not informed.
In the case where 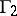 is repeated indefinitely, the extent to which player
is repeated indefinitely, the extent to which player  is informed about the interests and possibilities of player
is informed about the interests and possibilities of player 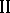 can be increased because of the information contained in the responses of player
can be increased because of the information contained in the responses of player 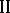 to the action of player
to the action of player 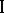 . Procedures are accordingly constructed that allow player
. Procedures are accordingly constructed that allow player 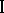 , starting with some play, to obtain a result arbitrarily close to the result guaranteed to him by complete information. Such results are also obtained in a game
, starting with some play, to obtain a result arbitrarily close to the result guaranteed to him by complete information. Such results are also obtained in a game  with indefiniteness. If the moments when player
with indefiniteness. If the moments when player 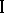 obtains information on the indeterminate factors
obtains information on the indeterminate factors  are not fixed, then player
are not fixed, then player 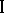 can obtain in the remaining repetitions a result that is arbitrarily close to that guaranteed to him by complete information, under weaker assumptions on the pay-off functions of the participants. Moreover, player
can obtain in the remaining repetitions a result that is arbitrarily close to that guaranteed to him by complete information, under weaker assumptions on the pay-off functions of the participants. Moreover, player 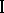 in
in 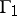 can obtain a similar result simply by observing the values of his own pay-off function.
can obtain a similar result simply by observing the values of his own pay-off function.
The formulations of the games under consideration carry over naturally to the case of many persons whose interactions, in the sense of priority of action and transfer of information, have a hierarchy structure. In analyzing these games it is necessary to stipulate a rule of interaction of the players on the same level. Thus, when three-person games are considered, where the pay-off functions of the players have the form
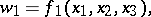 |
 |
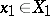 ,
, 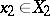 ,
, 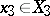 , then in order to describe the largest guaranteed result of a chosen player
, then in order to describe the largest guaranteed result of a chosen player 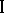 who has priority of action, it is necessary to make concrete his information on the behaviour of the players
who has priority of action, it is necessary to make concrete his information on the behaviour of the players 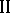 and
and  . If
. If 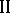 and
and  form a rigid coalition to the knowledge of
form a rigid coalition to the knowledge of 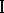 , that is, they formulate coalition criteria and determine their choices together, this case is equivalent to the previous two-person games as far as
, that is, they formulate coalition criteria and determine their choices together, this case is equivalent to the previous two-person games as far as  is concerned. Clear results have been obtained also in the case where the players
is concerned. Clear results have been obtained also in the case where the players  and
and  either are in a coalition known to player
either are in a coalition known to player 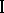 or act as individuals if they can then obtain a better result than is given by coalition; in this case neither player
or act as individuals if they can then obtain a better result than is given by coalition; in this case neither player 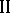 nor player
nor player  has independent information on the moves of the other, and the order of these moves is given by player
has independent information on the moves of the other, and the order of these moves is given by player 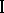 . Games having a "fan" structure have been analyzed in detail: a distinguished player
. Games having a "fan" structure have been analyzed in detail: a distinguished player 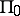 (who controls the centre) and
(who controls the centre) and  other players on the next level in the hierarchy (the producers of the output) tend to an increase in the pay-off functions
other players on the next level in the hierarchy (the producers of the output) tend to an increase in the pay-off functions 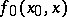 and
and 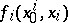 ,
, 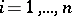 , respectively, where
, respectively, where 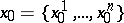 is the choice of
is the choice of 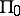 ,
, 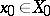 ,
, 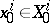 , and
, and 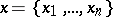 is the set of choices of the players on the lower level of the hierarchy, who act moreover, independently, and the player with index
is the set of choices of the players on the lower level of the hierarchy, who act moreover, independently, and the player with index 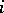 deals with the choice
deals with the choice 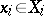 . All sets are assumed to be compact and the functions to be continuous. Player
. All sets are assumed to be compact and the functions to be continuous. Player 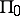 expects information (and will have it) on the choices
expects information (and will have it) on the choices 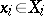 and informs every player
and informs every player 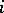 of the corresponding strategy function
of the corresponding strategy function  defined on
defined on 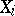 with values in
with values in 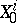 . For
. For  -person games with a hierarchy structure, expressions have been obtained for the largest guaranteed result of the distinguished player under various extensions of his class of strategies, at the expense of transmitting to the players on lower levels information on the actions of their colleagues, as well of of introducing actions of their colleagues and elements of bluff. As with games for two persons, the possibility of side payments to the distinguished player simplifies the determination of his guaranteed result considerably.
-person games with a hierarchy structure, expressions have been obtained for the largest guaranteed result of the distinguished player under various extensions of his class of strategies, at the expense of transmitting to the players on lower levels information on the actions of their colleagues, as well of of introducing actions of their colleagues and elements of bluff. As with games for two persons, the possibility of side payments to the distinguished player simplifies the determination of his guaranteed result considerably.
Using games with a hierarchy structure, a natural interpretation has been obtained of the various mechanisms of centralized control of active economic subsystems. The game 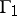 describes the process of centralized control by means of prices;
describes the process of centralized control by means of prices; 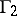 models the policy of penalties and encouragement via stimulation of production; and
models the policy of penalties and encouragement via stimulation of production; and  models the process of resource distribution as a function of the industrial methods of using these resources.
models the process of resource distribution as a function of the industrial methods of using these resources.
References
| [1] | Yu.B. Germeier, "Non-antagonistic games" , Reidel (1986) (Translated from Russian) |
Comments
Game  is often referred to as a Stackelberg game. In the formulation given, player
is often referred to as a Stackelberg game. In the formulation given, player 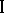 is the leader who conveys his decision to player
is the leader who conveys his decision to player 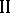 , the follower, who makes his decision afterwards. See [a1], Chapt. IV. In the economic literature, game
, the follower, who makes his decision afterwards. See [a1], Chapt. IV. In the economic literature, game 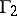 is said to have an incentive structure. Player
is said to have an incentive structure. Player 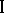 , the leader again, does not announce his action, but instead his strategy to player
, the leader again, does not announce his action, but instead his strategy to player 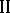 . The decision of player
. The decision of player  then also determines the action (i.e. decision) of player
then also determines the action (i.e. decision) of player 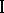 ; player
; player 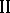 's decision is substituted into player
's decision is substituted into player 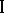 's strategy, which results in player
's strategy, which results in player 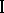 's decision [a2].
's decision [a2].
References
| [a1] | T. Basar, G.J. Olsder, "Dynamic noncooperative game theory" , Acad. Press (1982) |
| [a2] | P.B. Luk, Y.C. Ho, G.J. Olsder, "A control-theoretical view on incentives" Automatica , 18 (1982) pp. 167–179 |
Game with a hierarchy structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Game_with_a_hierarchy_structure&oldid=11264