Wall group
An Abelian group associated with a ring with an involution which is an anti-isomorphism. In particular, it is defined for any group ring 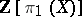 , where
, where 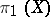 is the fundamental group of a space. If
is the fundamental group of a space. If 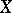 is a Poincaré complex, then for a bordism class
is a Poincaré complex, then for a bordism class 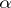 in
in 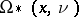 there is an obstruction in this group to the existence of a simple homotopy equivalence in
there is an obstruction in this group to the existence of a simple homotopy equivalence in 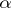 . This obstruction is called the Wall invariant, cf. [1].
. This obstruction is called the Wall invariant, cf. [1].
Let 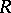 be a ring with an involution
be a ring with an involution 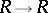 which is an anti-isomorphism, i.e.
which is an anti-isomorphism, i.e.  . If
. If 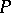 is a left
is a left 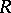 -module, then
-module, then 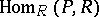 is a left
is a left 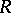 -module relative to the action
-module relative to the action 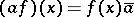 ,
, 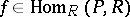 ,
, 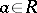 ,
, 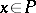 . This module is denoted by
. This module is denoted by 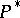 . For a finitely-generated projective
. For a finitely-generated projective  -module
-module 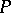 there is an isomorphism
there is an isomorphism 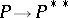 :
: 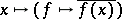 , and one may identify
, and one may identify 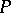 and
and 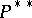 using this isomorphism.
using this isomorphism.
A quadratic 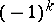 -form over a ring
-form over a ring 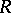 with an involution is a pair
with an involution is a pair  , where
, where 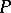 is a finitely-generated projective
is a finitely-generated projective 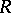 -module and
-module and 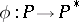 is a homomorphism such that
is a homomorphism such that 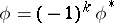 . A morphism
. A morphism 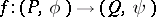 of forms is a homomorphism
of forms is a homomorphism 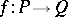 such that
such that 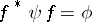 . If
. If  is an isomorphism, then the form
is an isomorphism, then the form 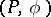 is said to be non-degenerate. A Lagrange plane of a non-degenerate form is a direct summand
is said to be non-degenerate. A Lagrange plane of a non-degenerate form is a direct summand 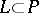 for which
for which  . If
. If 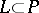 is a direct summand such that
is a direct summand such that 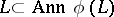 , then
, then 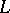 is called a subLagrange plane. Two Lagrange planes
is called a subLagrange plane. Two Lagrange planes  of a form
of a form 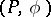 are called complementary if
are called complementary if 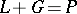 and
and 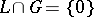 .
.
Let 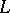 be a projective
be a projective 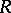 -module. The non-degenerate
-module. The non-degenerate 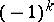 -form
-form
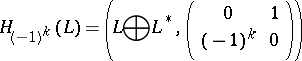 |
is called Hamiltonian, and 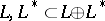 are called its complementary Lagrange planes. If
are called its complementary Lagrange planes. If 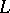 is a Lagrange plane of the form
is a Lagrange plane of the form 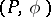 , then the form is isomorphic to the Hamiltonian form
, then the form is isomorphic to the Hamiltonian form 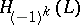 . The choice of a Lagrange plane complementary to
. The choice of a Lagrange plane complementary to 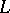 is equivalent to the choice of an isomorphism
is equivalent to the choice of an isomorphism 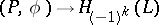 , and this complementary plane can be identified with
, and this complementary plane can be identified with 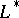 .
.
Let 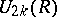 be the Abelian group generated by the equivalence classes (under isomorphism) of non-degenerate quadratic
be the Abelian group generated by the equivalence classes (under isomorphism) of non-degenerate quadratic 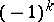 -forms
-forms 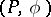 with the relations: 1)
with the relations: 1) 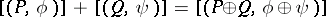 ; and 2)
; and 2) 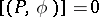 if
if 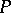 has a Lagrange plane. A triple
has a Lagrange plane. A triple  consisting of a non-degenerate
consisting of a non-degenerate 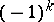 -form
-form 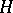 and a pair of Lagrange planes is called a
and a pair of Lagrange planes is called a 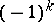 -formation. A formation is said to be trivial if
-formation. A formation is said to be trivial if 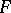 and
and 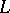 are complementary, and elementary if there exists a Lagrange plane of
are complementary, and elementary if there exists a Lagrange plane of 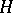 which is complementary to both
which is complementary to both 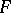 and
and 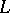 . The trivial formation
. The trivial formation 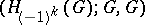 is called Hamiltonian. By an isomorphism of formations,
is called Hamiltonian. By an isomorphism of formations, 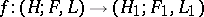 , one understands an isomorphism
, one understands an isomorphism 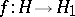 of forms for which
of forms for which  ,
, 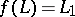 . Every trivial formation is isomorphic to the Hamiltonian one.
. Every trivial formation is isomorphic to the Hamiltonian one.
Let 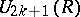 be the Abelian group generated by the equivalence classes (under isomorphism) of
be the Abelian group generated by the equivalence classes (under isomorphism) of 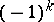 -formations with the following relations: a)
-formations with the following relations: a) 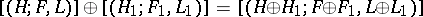 ; b)
; b) 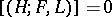 if the formation is elementary or trivial.
if the formation is elementary or trivial.
The groups 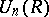 are called the Wall groups of the ring
are called the Wall groups of the ring 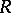 .
.
References
| [1] | C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) |
| [2] | A.A. Ranicki, "The algebraic theory of surgery I" Proc. London Math. Soc. , 40 : 1 (1980) pp. 87–192 |
Comments
In the case of 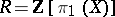 and the Wall surgery obstruction invariant, the involution on
and the Wall surgery obstruction invariant, the involution on 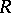 is given by
is given by 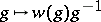 ,
, 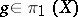 , where the group homomorphism
, where the group homomorphism 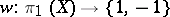 is given by the first Stiefel–Whitney class of the bundle
is given by the first Stiefel–Whitney class of the bundle  in the bordism class
in the bordism class 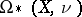 .
.
The Wall groups  are more often called
are more often called 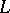 -groups and denoted by
-groups and denoted by 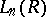 ; their theory is referred to as
; their theory is referred to as 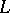 -theory, which is much related to
-theory, which is much related to 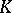 -theory. (Indeed, some authors speak of the
-theory. (Indeed, some authors speak of the 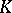 -theory of forms, [a2].) The
-theory of forms, [a2].) The 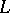 -groups are four-periodic, i.e.
-groups are four-periodic, i.e. 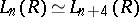 .
. 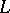 -groups can be defined in more general situations and there are a number of somewhat different varieties of
-groups can be defined in more general situations and there are a number of somewhat different varieties of  -groups, cf. e.g. [a1], [a2].
-groups, cf. e.g. [a1], [a2].
References
| [a1] | A. Ranicki, "Lower 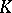 - and - and  -theory" , Cambridge Univ. Press (1992) -theory" , Cambridge Univ. Press (1992) |
| [a2] | A. Bak, "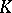 -theory of forms" , Princeton Univ. Press (1981) -theory of forms" , Princeton Univ. Press (1981) |
Wall group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wall_group&oldid=11262