Conjugate directions
From Encyclopedia of Mathematics
A pair of directions emanating from a point 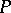 on a surface
on a surface 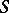 such that the straight lines containing them are conjugate diameters of the Dupin indicatrix of
such that the straight lines containing them are conjugate diameters of the Dupin indicatrix of 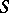 at
at 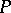 . In order that the directions
. In order that the directions 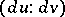 ,
, 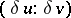 at a point
at a point 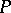 on
on 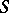 be conjugate, it is necessary and sufficient that the following condition holds
be conjugate, it is necessary and sufficient that the following condition holds
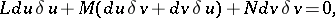 |
where 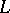 ,
, 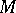 and
and 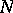 are the coefficients of the second fundamental form of
are the coefficients of the second fundamental form of 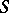 evaluated at
evaluated at 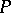 . Example: a principal direction.
. Example: a principal direction.
References
| [1] | A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian) |
Comments
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , 1 , Springer (1973) |
| [a2] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Conjugate directions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_directions&oldid=11253
Conjugate directions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_directions&oldid=11253
This article was adapted from an original article by E.V. Shikin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article