Reductive space
A homogeneous space 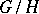 of a connected Lie group
of a connected Lie group 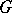 such that in the Lie algebra
such that in the Lie algebra 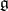 of
of 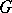 there is an
there is an 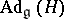 -invariant subspace complementary to the subalgebra
-invariant subspace complementary to the subalgebra  , where
, where  is the Lie algebra of the group
is the Lie algebra of the group 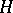 . The validity of any of the following conditions is sufficient for the homogeneous space
. The validity of any of the following conditions is sufficient for the homogeneous space 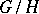 to be reductive: 1) the linear group
to be reductive: 1) the linear group  is completely reducible; or 2) in
is completely reducible; or 2) in 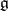 there is an
there is an 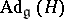 -invariant bilinear form whose restriction to
-invariant bilinear form whose restriction to  is non-degenerate. In particular, any homogeneous Riemannian space is reductive. If
is non-degenerate. In particular, any homogeneous Riemannian space is reductive. If 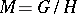 is a reductive space and the group
is a reductive space and the group 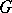 acts effectively on
acts effectively on 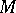 , then the linear representation of the isotropy group
, then the linear representation of the isotropy group 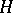 in the tangent space
in the tangent space 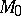 to the manifold
to the manifold 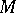 at the point
at the point 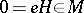 is faithful (cf. Faithful representation). Two important
is faithful (cf. Faithful representation). Two important 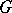 -invariant affine connections on
-invariant affine connections on 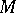 are associated with each
are associated with each 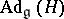 -invariant subspace
-invariant subspace 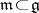 complementary to
complementary to 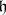 : the canonical connection and the natural torsion-free connection. The canonical connection on the reductive space
: the canonical connection and the natural torsion-free connection. The canonical connection on the reductive space 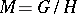 with a fixed
with a fixed 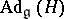 -invariant decomposition
-invariant decomposition 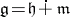 is the unique
is the unique 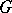 -invariant affine connection on
-invariant affine connection on 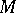 such that for any vector
such that for any vector 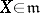 and any frame
and any frame  at the point 0, the curve
at the point 0, the curve  in the principal fibration of frames over
in the principal fibration of frames over 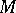 is horizontal. The canonical connection is complete and the set of its geodesics through 0 coincides with the set of curves of the type
is horizontal. The canonical connection is complete and the set of its geodesics through 0 coincides with the set of curves of the type 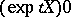 , where
, where  . After the natural identification of the spaces
. After the natural identification of the spaces 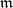 and
and 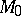 , the curvature tensor
, the curvature tensor 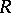 and torsion tensor
and torsion tensor 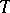 of the canonical connection are defined by the formulas
of the canonical connection are defined by the formulas 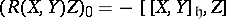 and
and 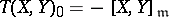 , where
, where 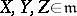 and
and 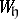 and
and 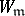 denote the projections of the vector
denote the projections of the vector 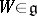 onto
onto 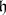 and
and  , respectively.
, respectively.
The tensor fields  and
and 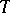 are parallel relative to the canonical connection, as is any other
are parallel relative to the canonical connection, as is any other 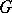 -invariant tensor field on
-invariant tensor field on  . The Lie algebra of the linear holonomy group (see Holonomy group) of the canonical connections on
. The Lie algebra of the linear holonomy group (see Holonomy group) of the canonical connections on 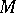 with supporting point 0 is generated by the set
with supporting point 0 is generated by the set 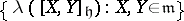 , where
, where 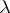 is the linear representation of the isotropy Lie algebra
is the linear representation of the isotropy Lie algebra 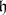 in the space
in the space 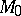 . Any connected simply-connected manifold with a complete affine connection with parallel curvature and torsion fields can be represented as a reductive space whose canonical connection coincides with the given affine connection. In the reductive space
. Any connected simply-connected manifold with a complete affine connection with parallel curvature and torsion fields can be represented as a reductive space whose canonical connection coincides with the given affine connection. In the reductive space 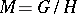 with fixed
with fixed 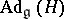 -invariant decomposition
-invariant decomposition 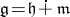 there is a unique
there is a unique 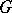 -invariant affine connection with zero torsion having the same geodesics as the canonical connection. This connection is called the natural torsion-free connection on
-invariant affine connection with zero torsion having the same geodesics as the canonical connection. This connection is called the natural torsion-free connection on 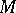 (relative to the decomposition
(relative to the decomposition 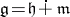 ). A homogeneous Riemannian or pseudo-Riemannian space
). A homogeneous Riemannian or pseudo-Riemannian space 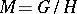 is naturally reductive if it admits an
is naturally reductive if it admits an  -invariant decomposition
-invariant decomposition 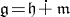 such that
such that
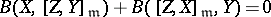 | (*) |
for all 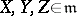 , where
, where 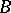 is the non-degenerate symmetric bilinear form on
is the non-degenerate symmetric bilinear form on 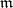 induced by the Riemannian (pseudo-Riemannian) structure on
induced by the Riemannian (pseudo-Riemannian) structure on 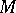 under the natural identification of the spaces
under the natural identification of the spaces 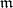 and
and 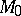 . If
. If 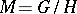 is a naturally reductive Riemannian or pseudo-Riemannian space with a fixed
is a naturally reductive Riemannian or pseudo-Riemannian space with a fixed 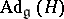 -invariant decomposition
-invariant decomposition 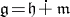 that satisfies condition (*), then the natural torsion-free connection coincides with the corresponding Riemannian or pseudo-Riemannian connection on
that satisfies condition (*), then the natural torsion-free connection coincides with the corresponding Riemannian or pseudo-Riemannian connection on 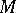 . If
. If  is a simply-connected naturally reductive homogeneous Riemannian space and
is a simply-connected naturally reductive homogeneous Riemannian space and 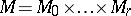 is its de Rham decomposition, then
is its de Rham decomposition, then  can be represented in the form
can be represented in the form 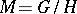 ; moreover,
; moreover, 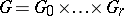 ,
, 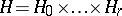 and
and 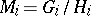
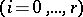 .
.
An important generalization of reductive spaces are  -reductive homogeneous spaces [4]. A homogeneous space
-reductive homogeneous spaces [4]. A homogeneous space 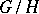 is called
is called  -reductive if its stationary subalgebra
-reductive if its stationary subalgebra 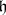 equals
equals  , where
, where 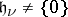 , and if there is a subspace
, and if there is a subspace  in
in 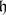 complementary to
complementary to 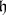 such that
such that 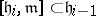 ,
, 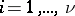 , where
, where 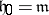 . The
. The 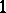 -reductive homogeneous spaces are in fact reductive spaces; examples of
-reductive homogeneous spaces are in fact reductive spaces; examples of  -reductive homogeneous spaces are projective (and conformal) spaces on which a group of projective (or conformal) transformations acts. If
-reductive homogeneous spaces are projective (and conformal) spaces on which a group of projective (or conformal) transformations acts. If 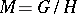 there is a
there is a  -reductive homogeneous space and if
-reductive homogeneous space and if 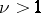 , then the linear representation of the isotropy Lie algebra
, then the linear representation of the isotropy Lie algebra  is not faithful (since
is not faithful (since 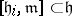 when
when 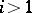 ); consequently, there is no
); consequently, there is no 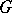 -invariant affine connection on
-invariant affine connection on 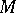 . However, there is a canonical
. However, there is a canonical 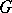 -invariant connection on a
-invariant connection on a  -reductive homogeneous space with the homogeneous space of some transitive-differential group of order
-reductive homogeneous space with the homogeneous space of some transitive-differential group of order  as fibre (see [4]). Reductive and
as fibre (see [4]). Reductive and  -reductive spaces are characterized as maximally homogeneous
-reductive spaces are characterized as maximally homogeneous 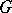 -structures (cf.
-structures (cf. 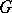 -structure) of appropriate type (cf. [6]).
-structure) of appropriate type (cf. [6]).
In addition to reductive spaces, partially reductive spaces are also examined, i.e. homogeneous spaces 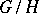 such that there is a decomposition of the Lie algebra
such that there is a decomposition of the Lie algebra 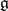 into a direct sum of two non-zero
into a direct sum of two non-zero 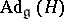 -invariant subspaces, one of which contains the subalgebra
-invariant subspaces, one of which contains the subalgebra 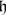 (see [5]).
(see [5]).
References
| [1] | S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 2 , Interscience (1969) |
| [2] | P.K. Rashevskii, "On the geometry of homogeneous spaces" Trudy Sem. Vektor. i Tenzor. Anal. , 9 (1952) pp. 49–74 |
| [3] | K. Nomizu, "Invariant affine connections on homogeneous spaces" Amer. J. Math. , 76 : 1 (1954) pp. 33–65 |
| [4] | I.L. Kantor, "Transitive differential groups and invariant connections in homogeneous spaces" Trudy Sem. Vektor. i Tenzor. Anal. , 13 (1966) pp. 310–398 |
| [5] | E.B. Vinberg, "Invariant linear connections in a homogeneous space" Trudy Moskov. Mat. Obshch. , 9 (1960) pp. 191–210 (In Russian) |
| [6] | D.V. Alekseevskii, "Maximally homogeneous  -structures and filtered Lie algebras" Soviet Math. Dokl. , 37 : 2 (1988) pp. 381–384 Dokl. Akad. Nauk SSSR , 299 : 3 (1988) pp. 521–526 -structures and filtered Lie algebras" Soviet Math. Dokl. , 37 : 2 (1988) pp. 381–384 Dokl. Akad. Nauk SSSR , 299 : 3 (1988) pp. 521–526 |
Comments
References
| [a1] | J.A. Wolf, "Spaces of constant curvature" , McGraw-Hill (1967) |
Reductive space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reductive_space&oldid=11232