Rational curve

A one-dimensional algebraic variety, defined over an algebraically closed field 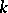, whose field of rational functions is a purely transcendental extension of degree 1 of . Every non-singular complete rational curve is isomorphic to the projective line . A complete singular curve 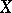is rational if and only if its geometric genus 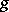is zero, that is, when there are no regular differential forms on .

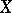When 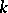is the field 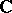of complex numbers, the (only) non-singular complete rational curve 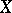is the Riemann sphere .

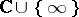Comments

In classic literature a rational curve is also called a unicursal curve.

If 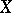is defined over a not necessarily algebraically closed field and is birationally equivalent to 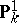over , 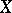is said to be a 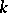-rational curve.

References

[a1]	W. Fulton, "Algebraic curves" , Benjamin (1969) pp. 66
[a2]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)